Analysis

Author

Steffi LaZerte

Published

September 5, 2025

Setup

source("XX_functions.R")  # Custom functions and packages

# Metrics
v <- read_csv("Data/Datasets/vultures_final.csv") |>
  # Round non-integer values of population counts
  mutate(across(c(contains("pop"), contains("raw")), round)) 

# Raw counts
raw <- read_csv("Data/Datasets/vultures_clean_2023.csv")

# Predicted GAM models
pred <- read_csv("Data/Datasets/vultures_gams_pred.csv")

Set plotting defaults

y_breaks <- seq(200, 300, by = 5)

Using This Report

This report contains all the stats and analyses for the final data set.

Each section (e.g., “Timing of kettle formation”) contains the analysis for a particular type of data.

These analyses have several parts

  1. Descriptive statistics - min, max, median, etc.
  2. Model results - results of linear or general linear models, depending on the measures
  3. Figures - visualizing the models on top of the data
  4. Model Checks - DHARMa plots assessing model fit and assumptions
  5. Sensitivity - Checking influential observations
  6. Full Model Results - the raw summary output of the models, for completeness

Models

Most models are standard linear regressions.

Some, involving the count data (number of birds) are either Negative binomial or Poisson generalized linear models.

The Patterns of migration (skew and kurtosis) are linear models without predictors (intercept only), which effectively makes them t-tests (they produce the exact same estimates and statistics), but allow us to use DHARMA for model checking, etc.

Model Results

Model results are presented in a tabulated form, which is also saved to CSV as Data/Tables/table_MEASURE.csv.

They are also presented as the “Full Model Results”. This is the output of using summary(model) in R and is just a complete version of the output in case anything needs to be inspected at a later date. In short, I don’t think you’ll need it, but I’ve included it just in case.

The tabulated results contain both estimates and P values, as well as overall model R2 values for linear models (but not for general linear models, as they don’t really apply). I could also add confidence intervals as well if that’s useful.

R2 values are presented as regular and adjusted. The adjusted values take into account samples sizes and the number of predictors.

We can interpret the Estimates directly, especially in linear models.

For example, if there is a significant effect of year on mig_start_doy, and the estimate is 0.176 we can say:

“There was a significant effect of year on the start date of kettle formations, such that the start date increased by 0.176 days per year (t = XXX; P-value = XXX). Thus kettle formations started ~4.4 days later at the end of the study compared to the start.”

Considering that there are 25 years in this study.

For Negative Binomial or Poisson models, we will transform the estimates to “Incident Rate Ratios” by exponentiating the estimate.

For example, if there is a significant effect of year on mig_pop_max in a generalized linear model with the negative binomial family, and the estimate is 0.03625499, we can first calculate the exponential:

exp(0.03625499)
[1] 1.03692

Then we can say:

“There was a significant effect of year on the maximum number of vultures predicted in a kettle (Est = 0.0363; t = XXX; P-value = XXX), such that the number of birds increased by 3% per year.”

If our exponentiated result was 3, we would say a “300% increase”, or a “3-fold” increase.

These exponentiated estimates are included in the outputs as well as “Estimate Exp”

Variables

All variables are generally referred to by their name in the data set, e.g., mig_start_doy.

See the glossary of variables names in the Calculate Metrics > Data Details section.

Figures

You can click on any figure expand it out.

These figures are here to demostrate the patterns we’re seeing in the data and the stats. I imagine you would want different figures for publication, so just let me know what they should look like!

DHARMa plots

DHARMa is a package for simulating residuals to allow model checking for all types of models (details).

Generally these plots can be interpreted similarly to interpreting QQ Normal and Residual plots for linear models (although technically they’re using simulated residuals, not model residuals).

For context…

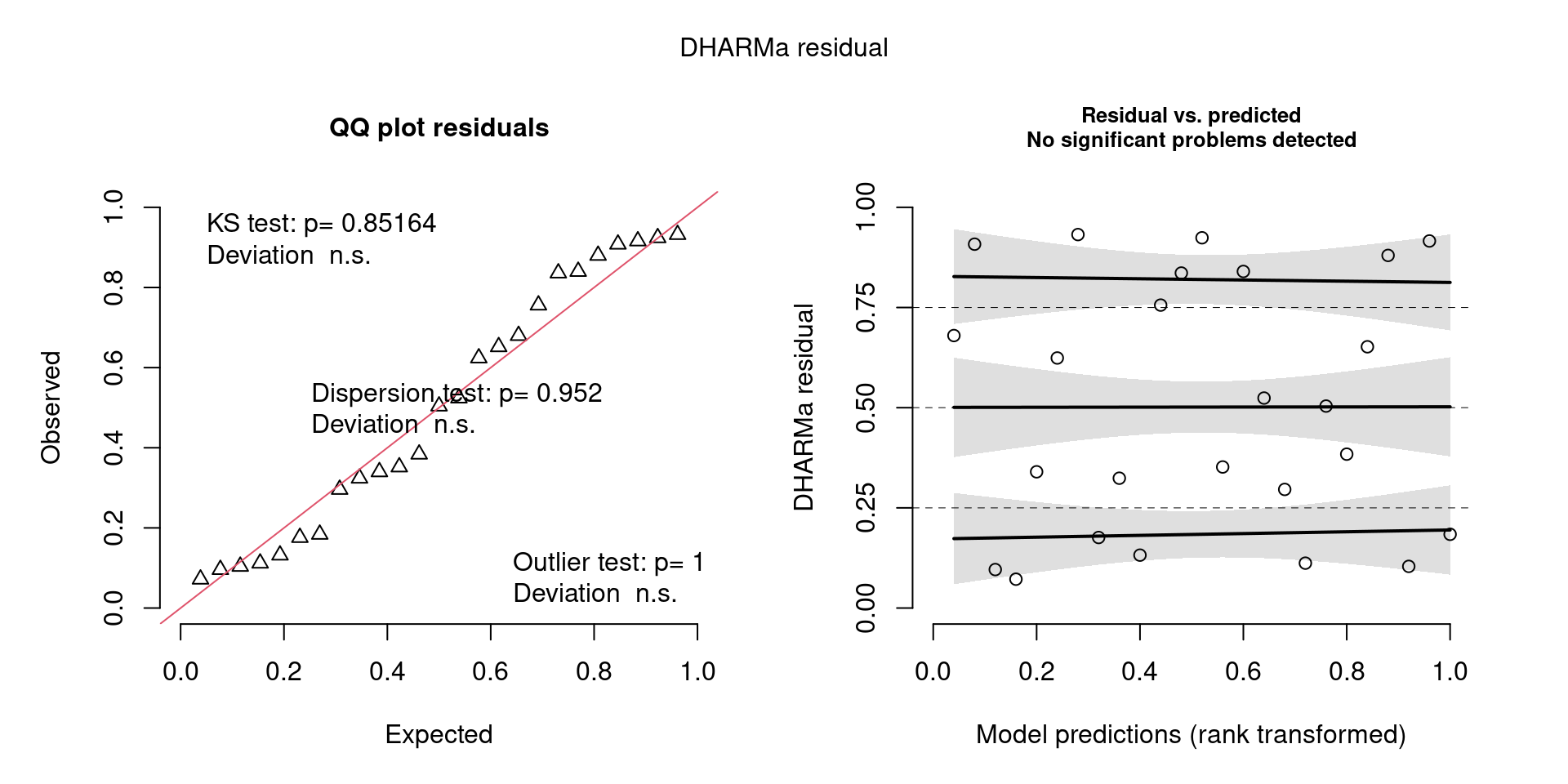
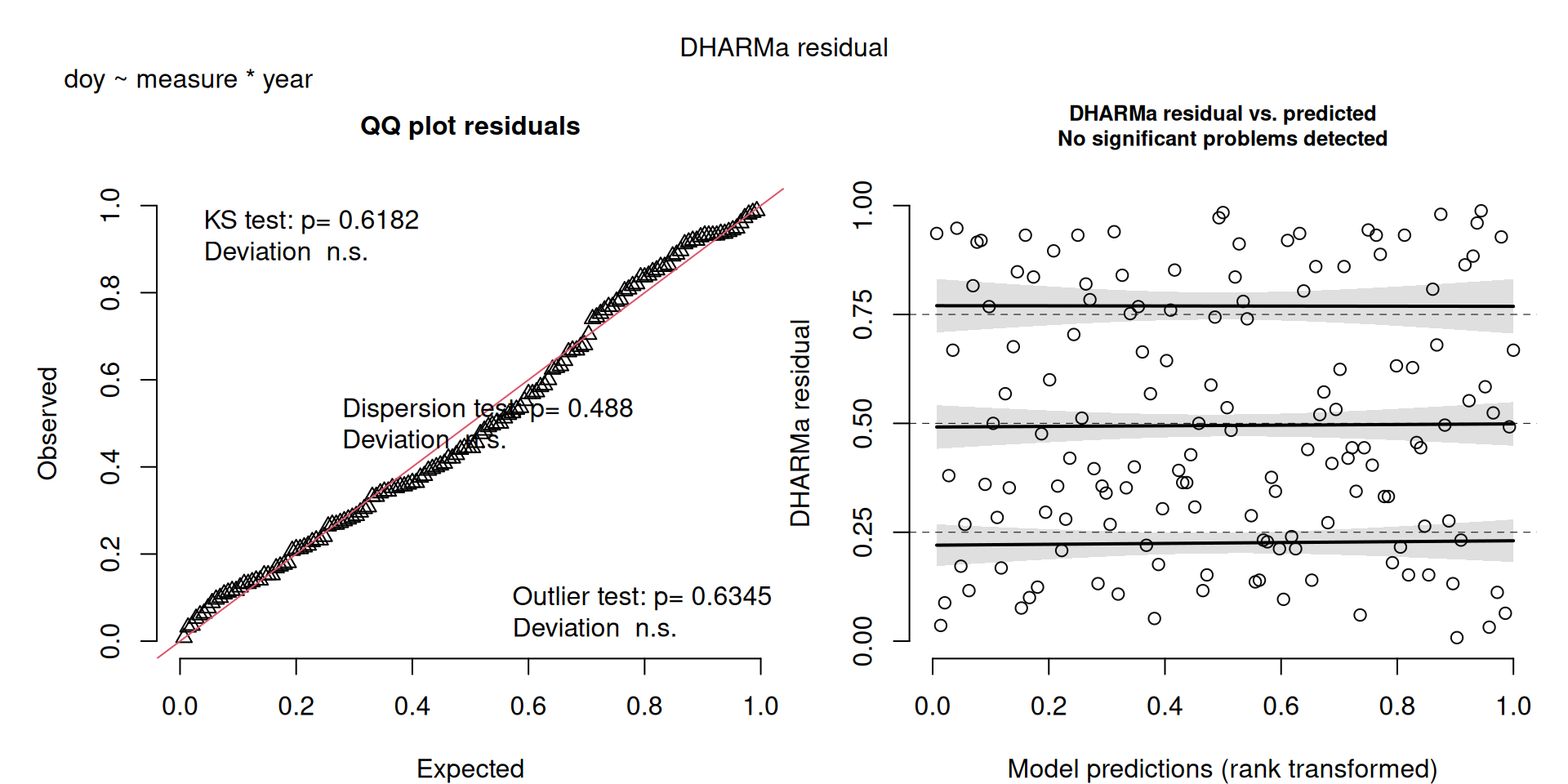
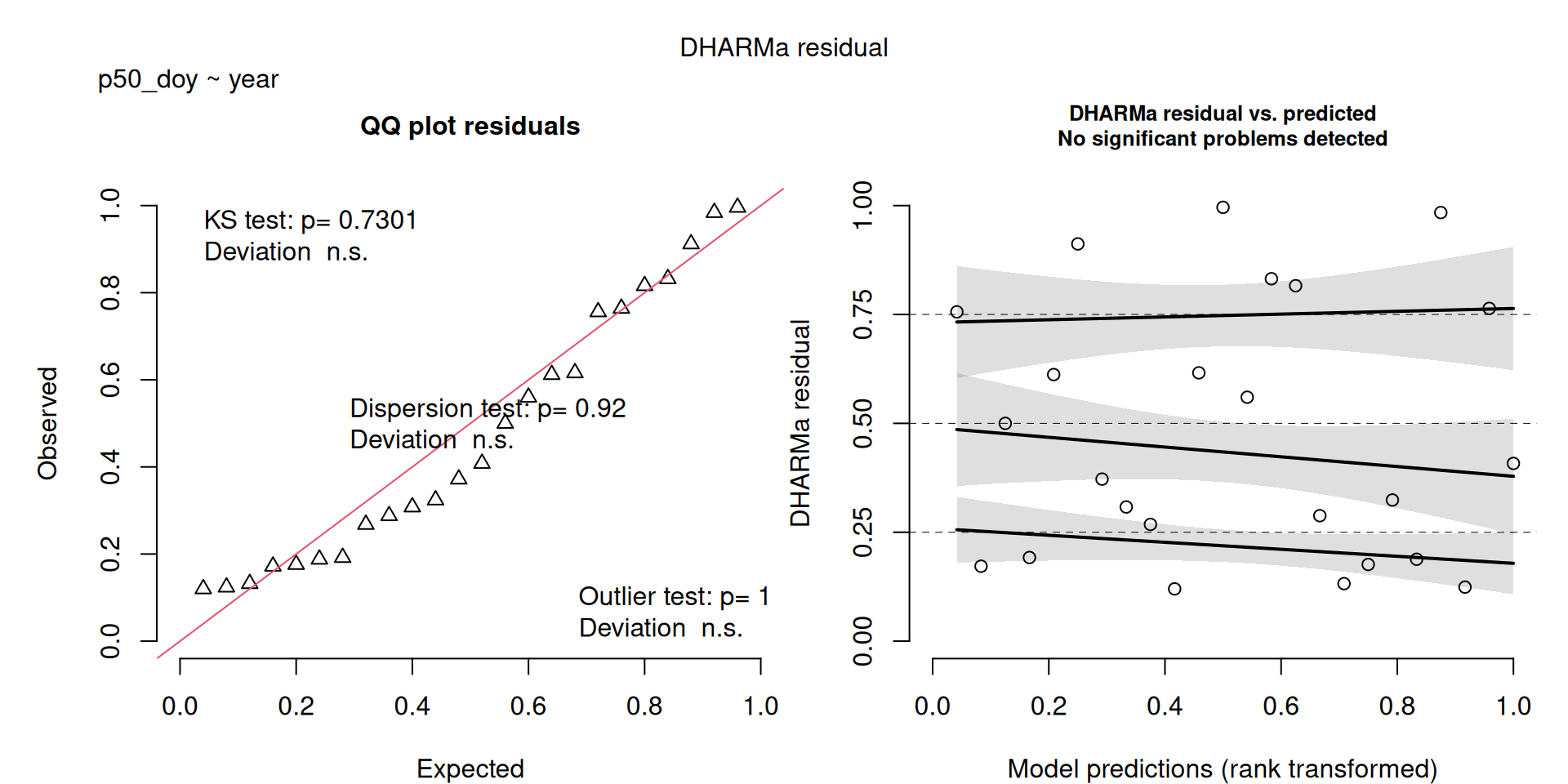
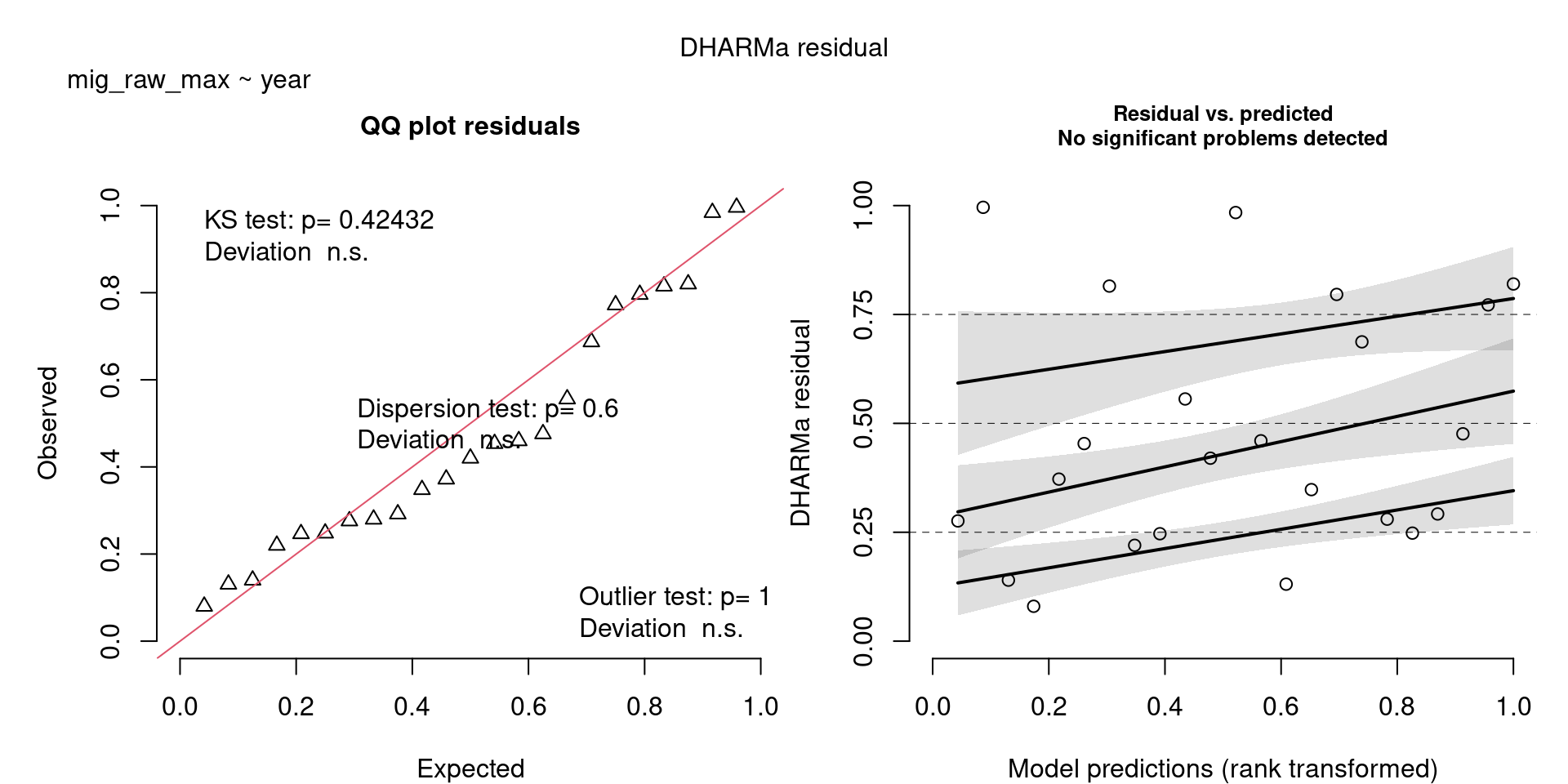
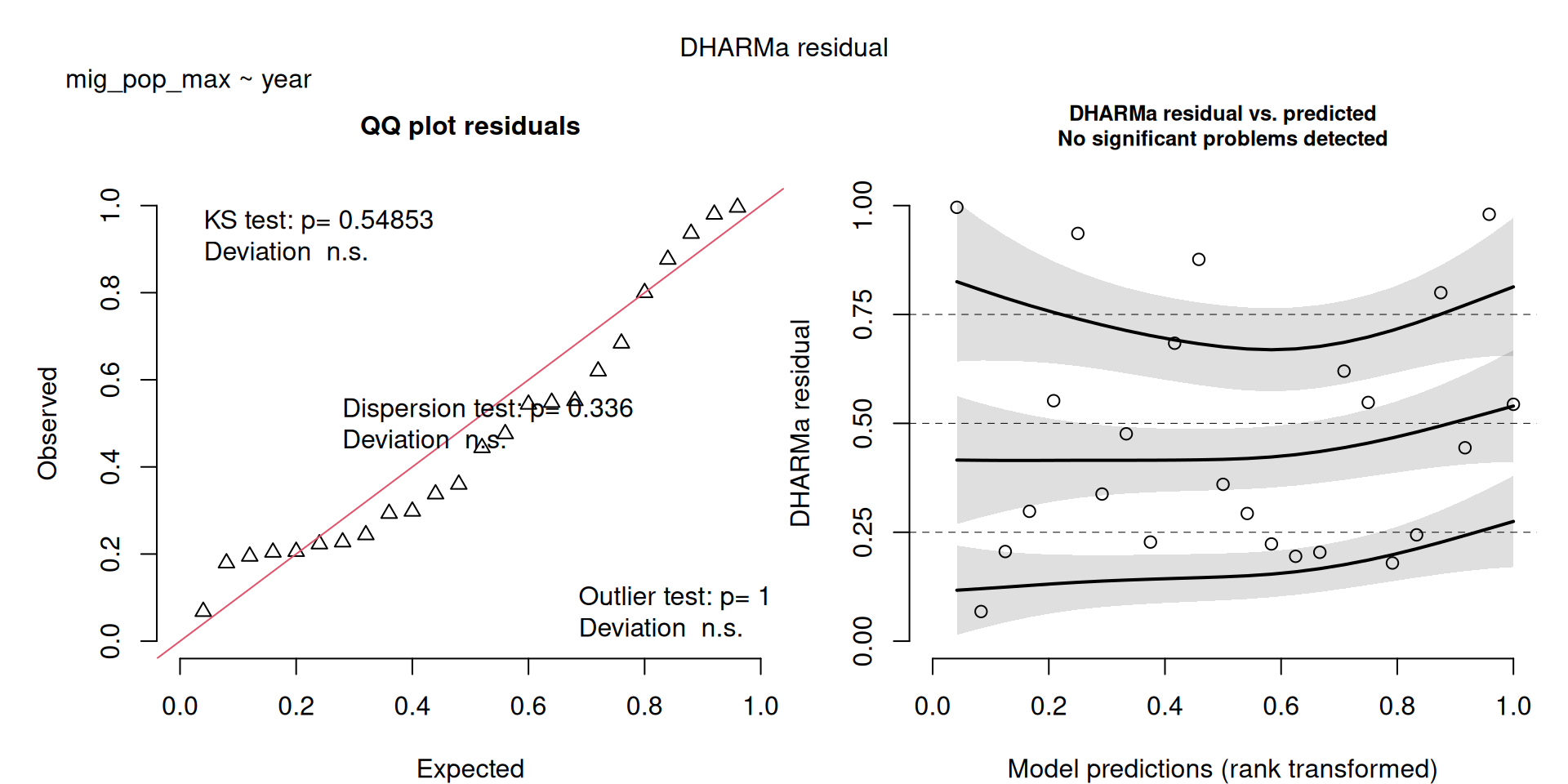
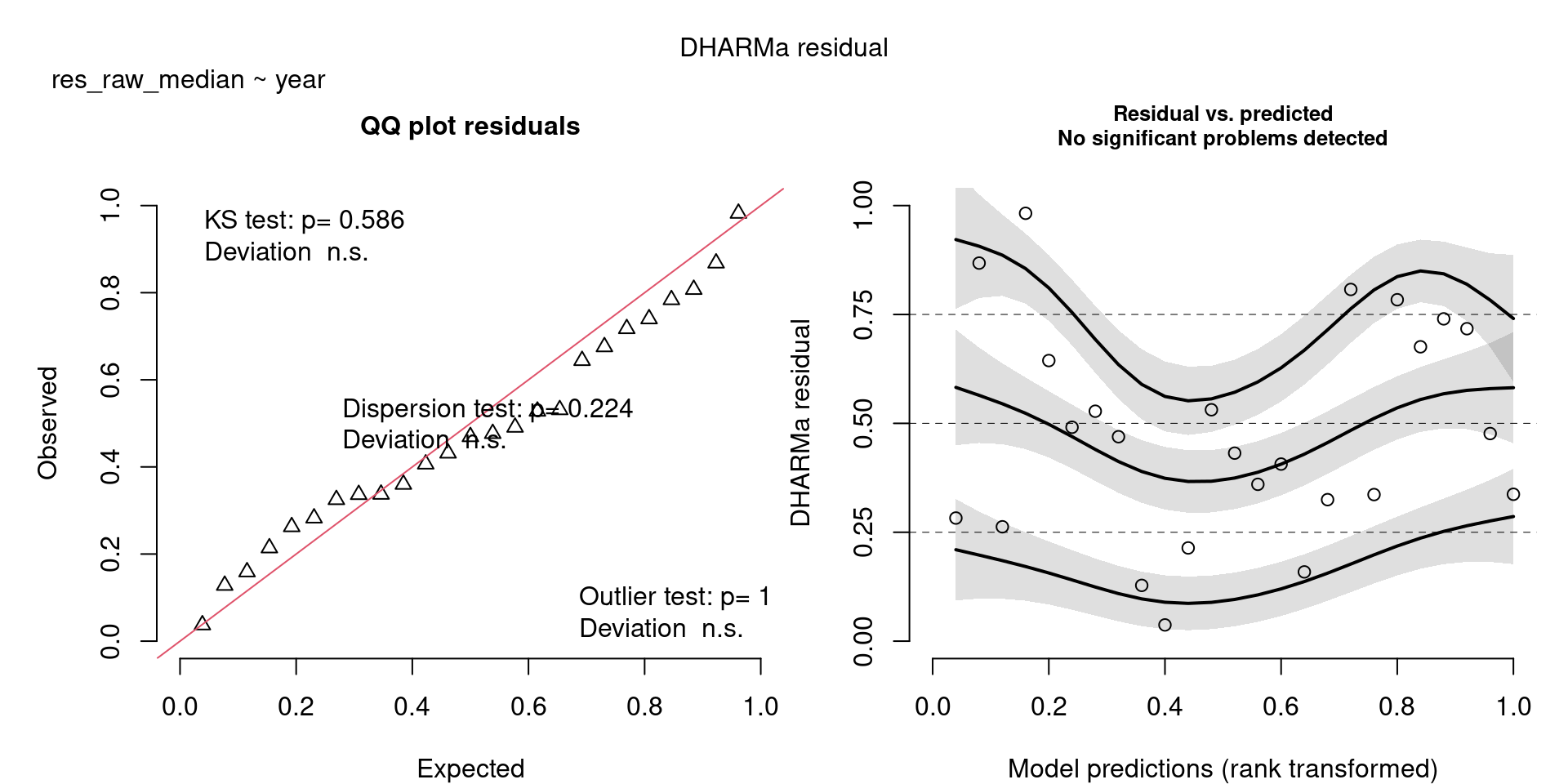
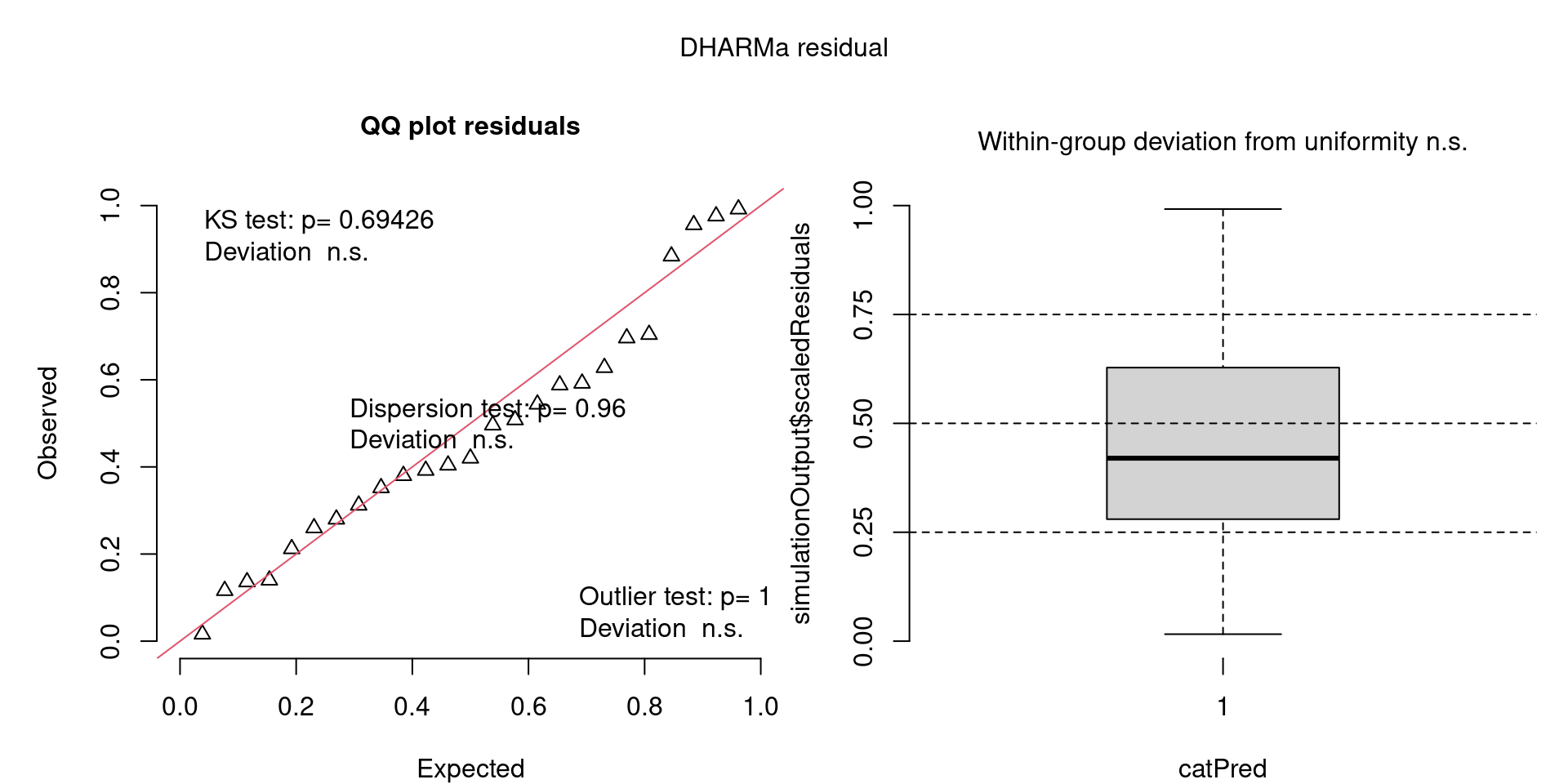
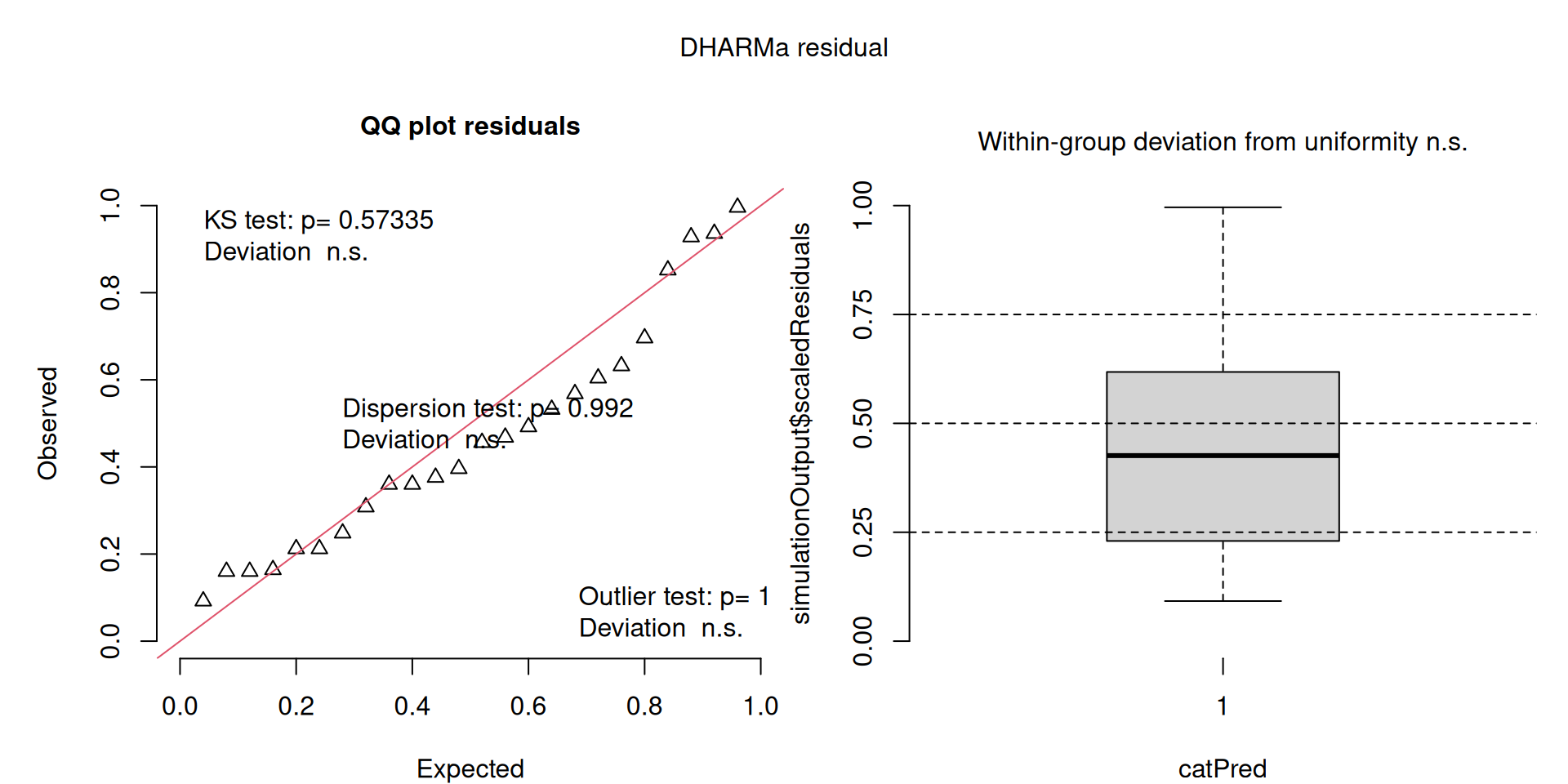
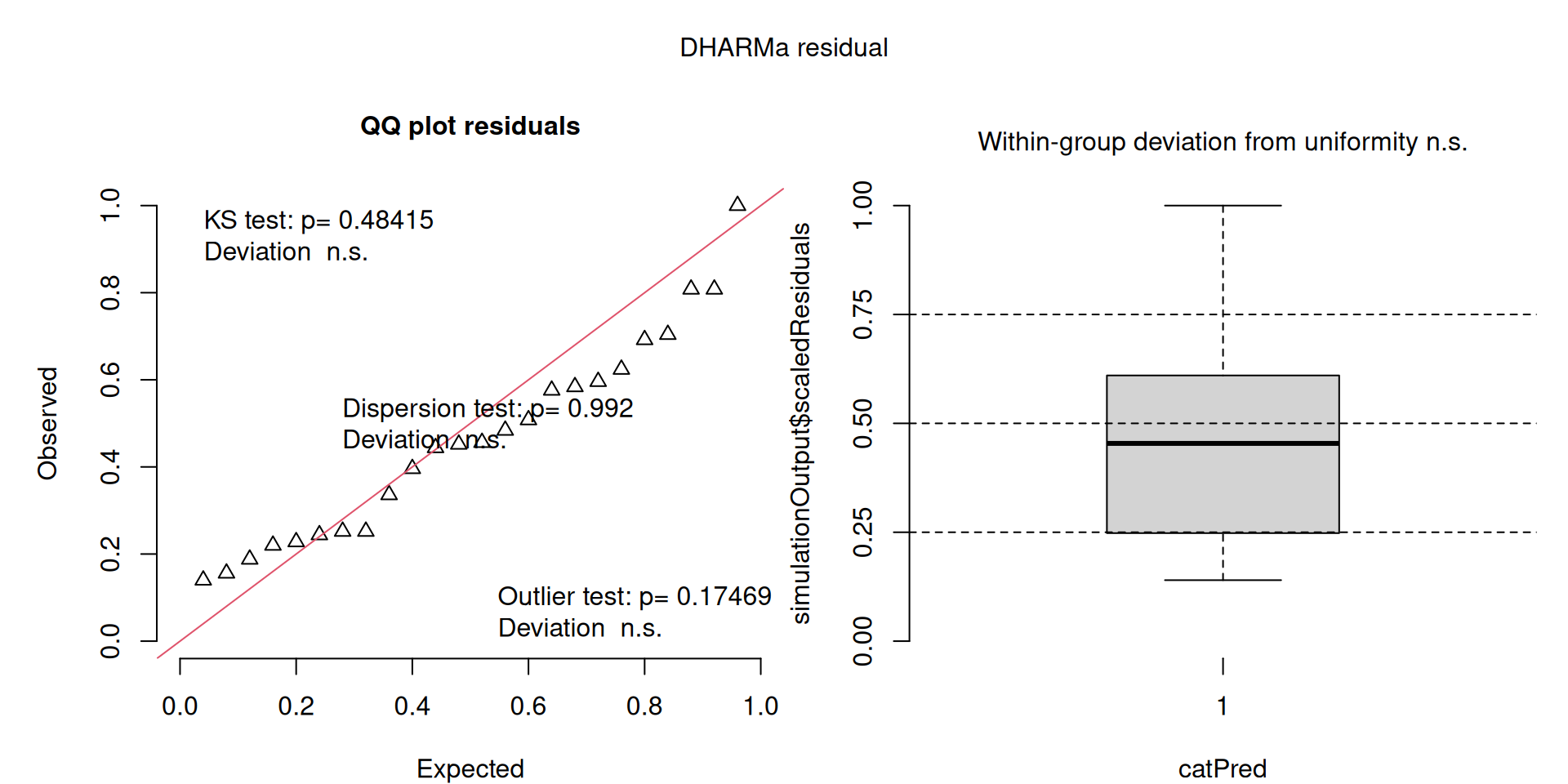
For example, we would interpret the following plot as showing decent model fit and assumptions.

The QQ plot on the left is nearly straight, there are no tests that flag problems in the distribution (KS test), Dispersion or Outliers. We also see no pattern in the residuals and no problems have been highlighted.

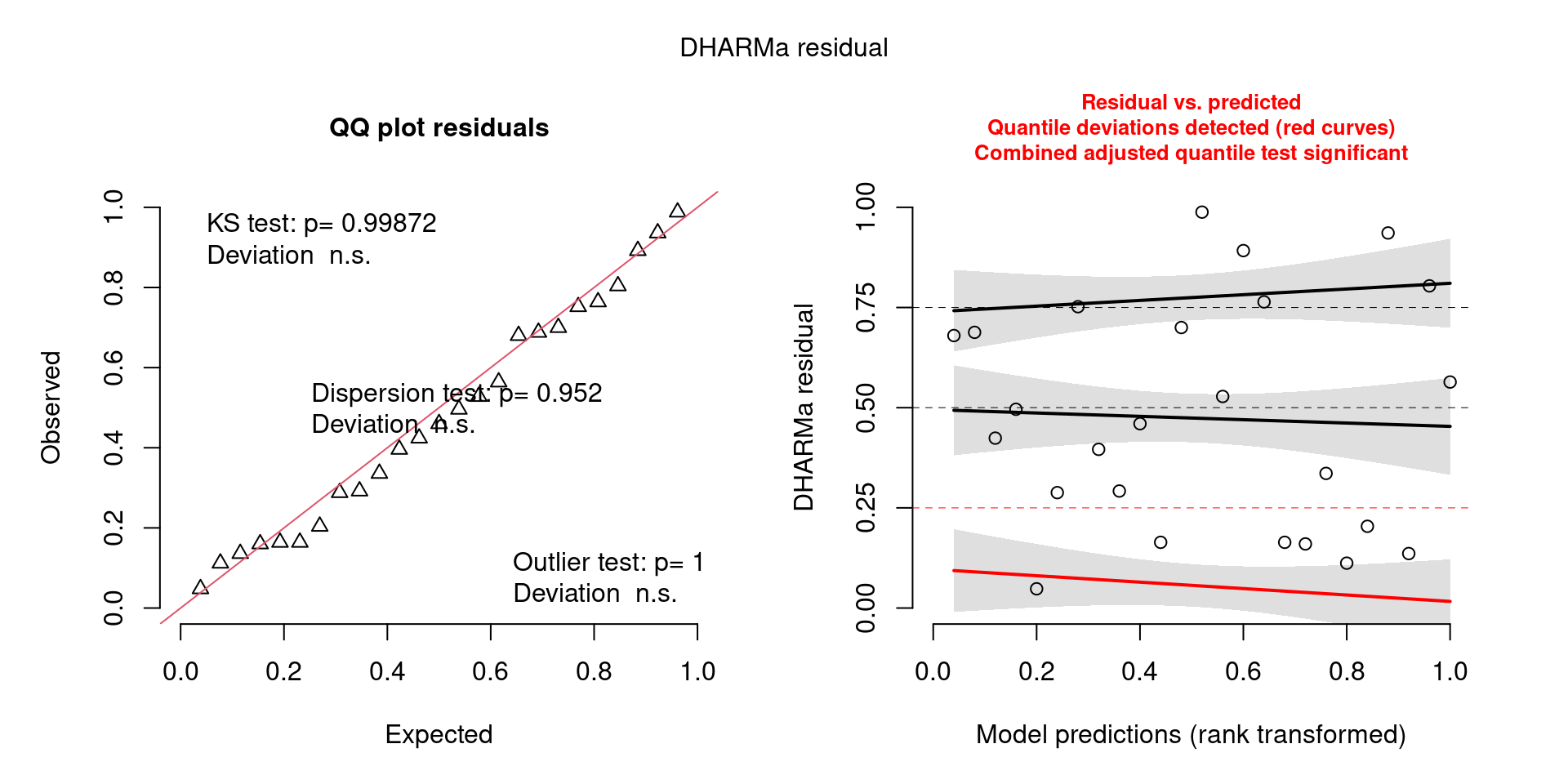
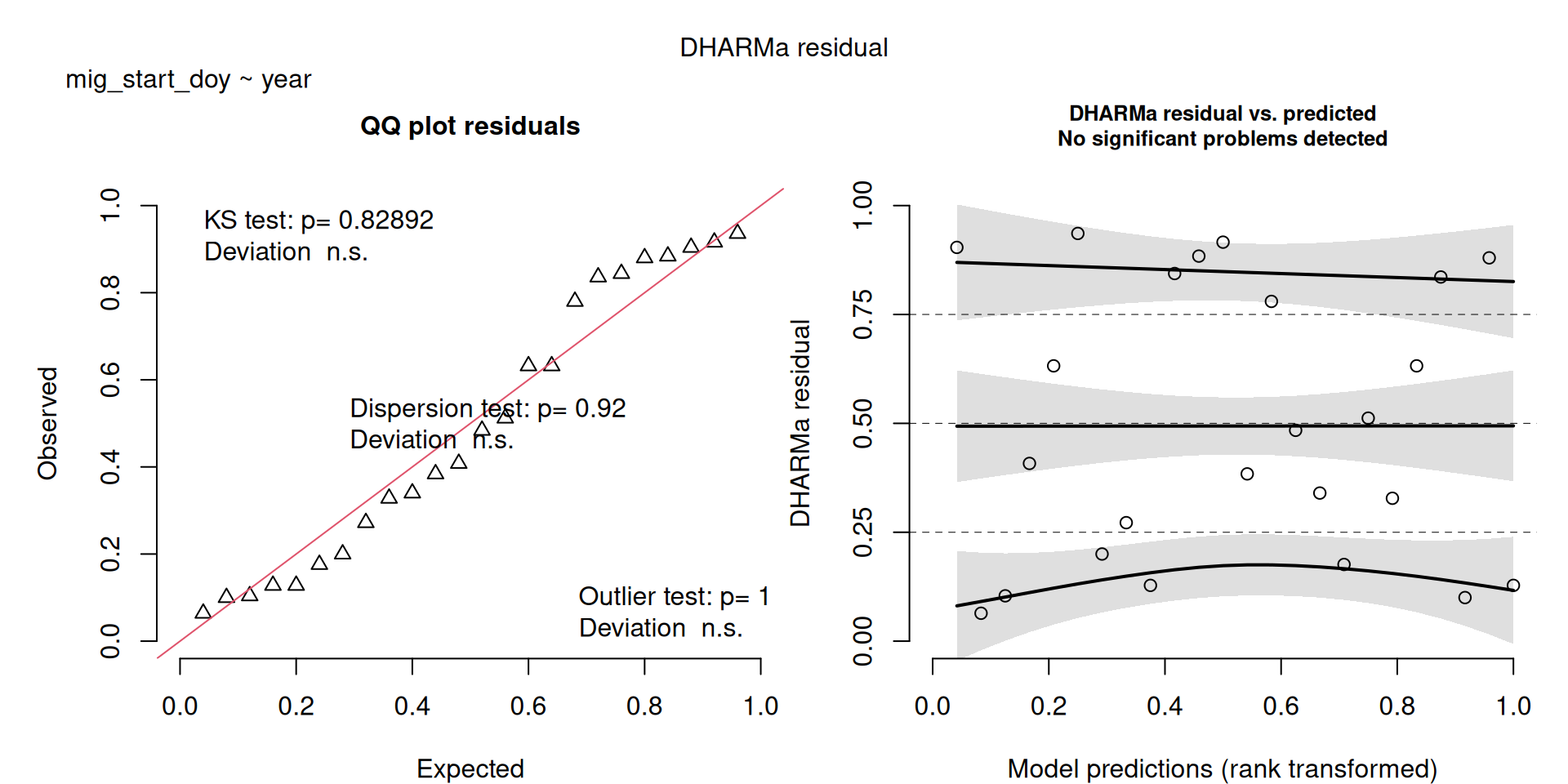
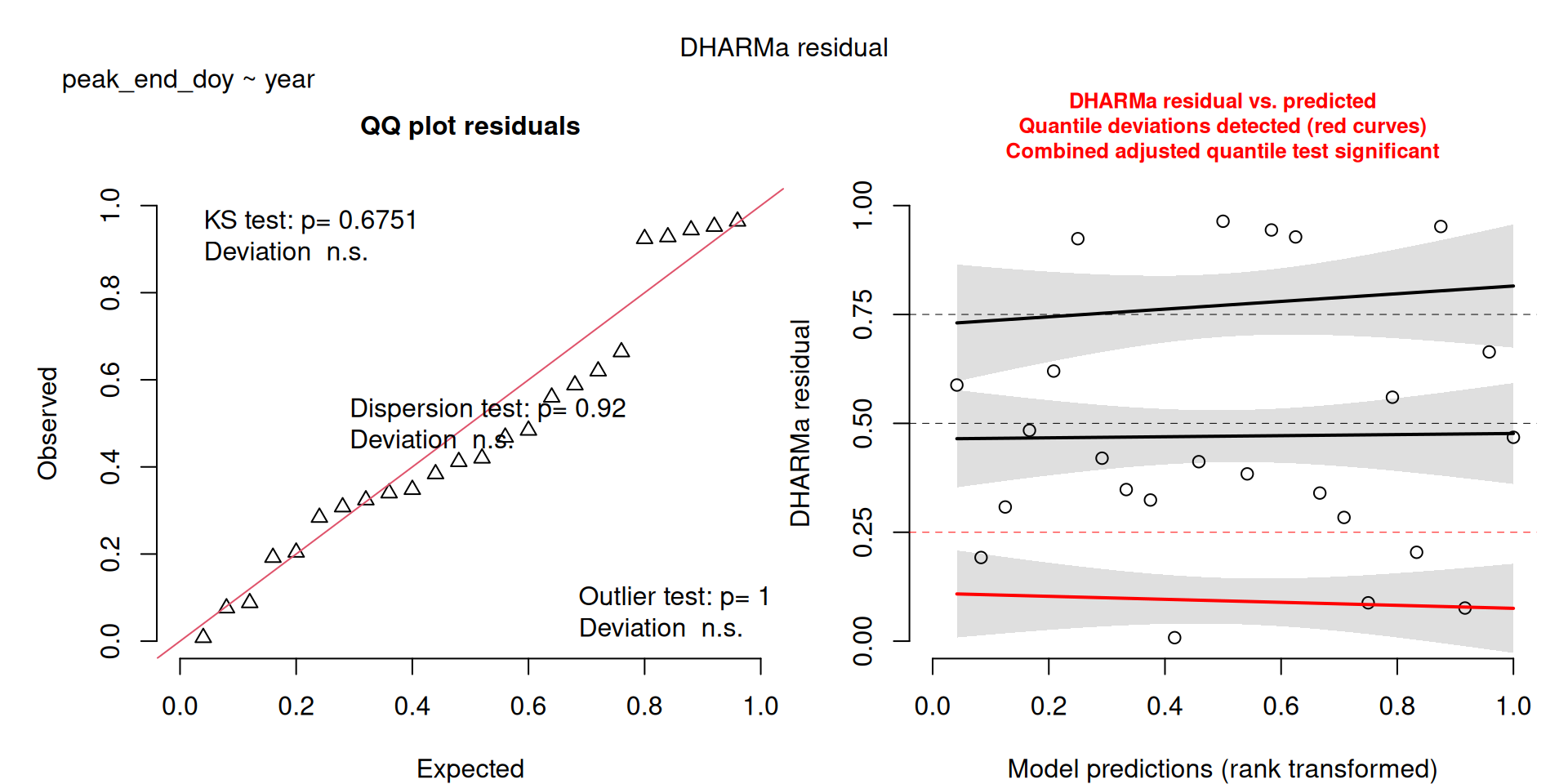
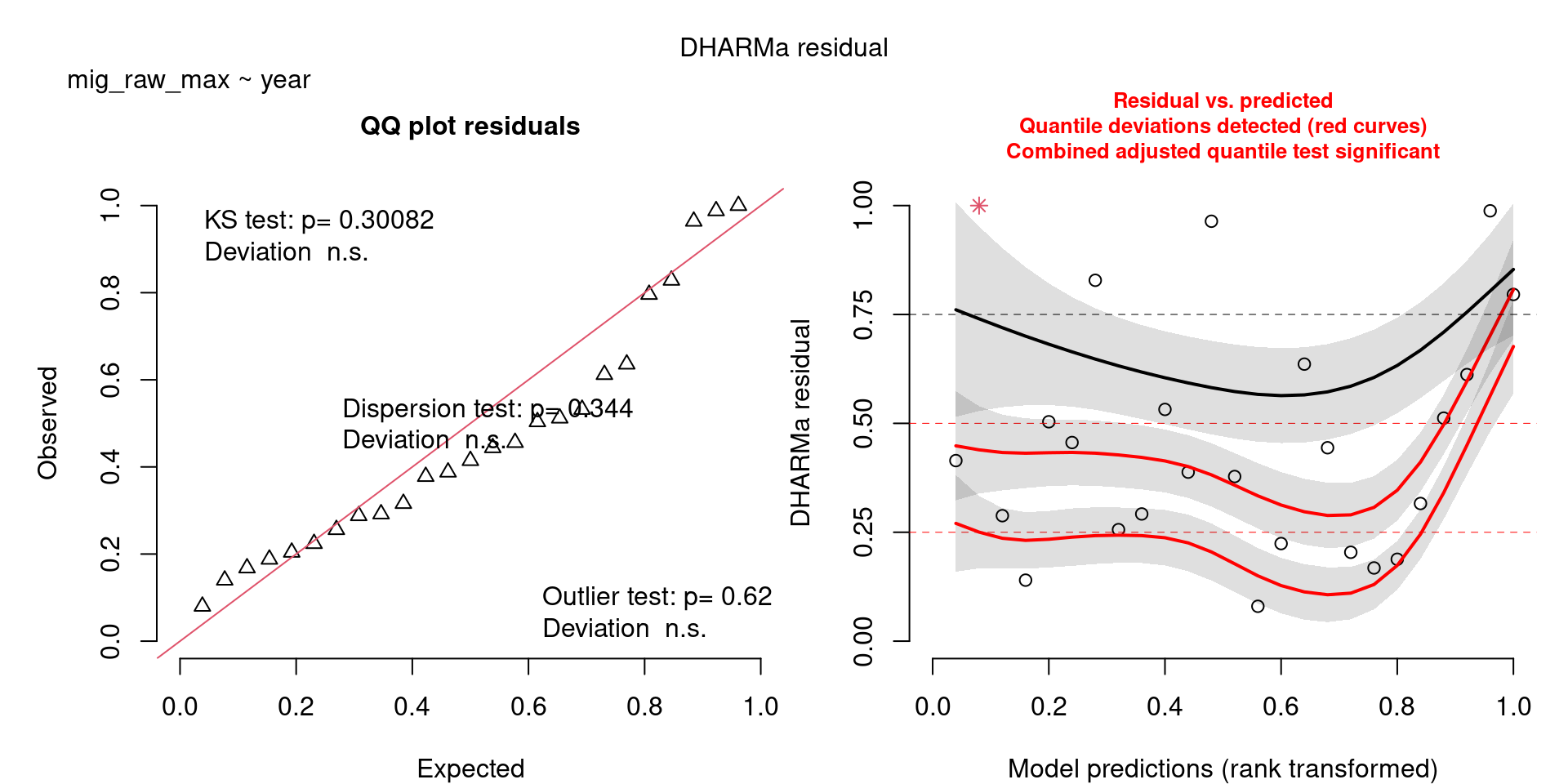
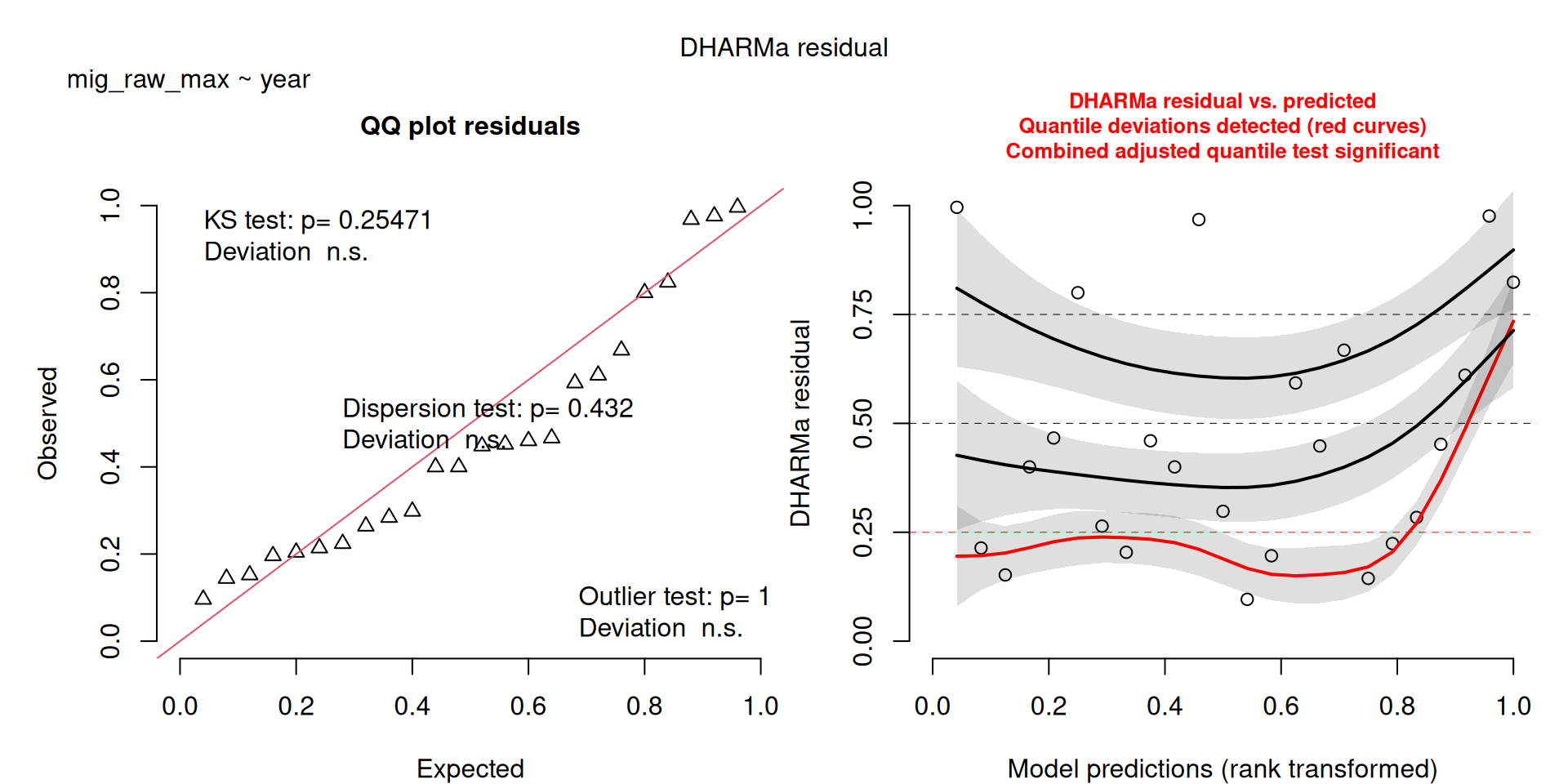
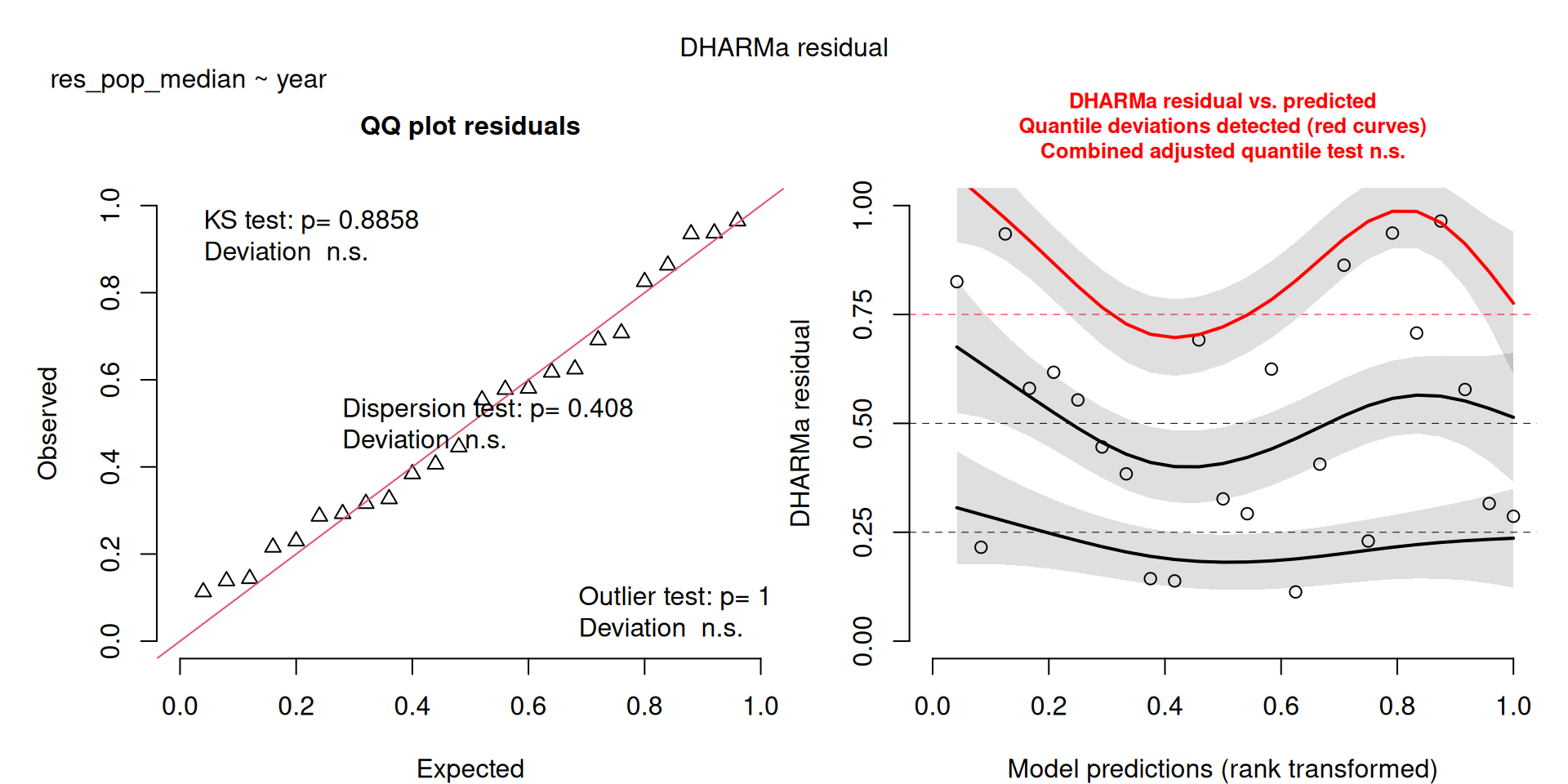
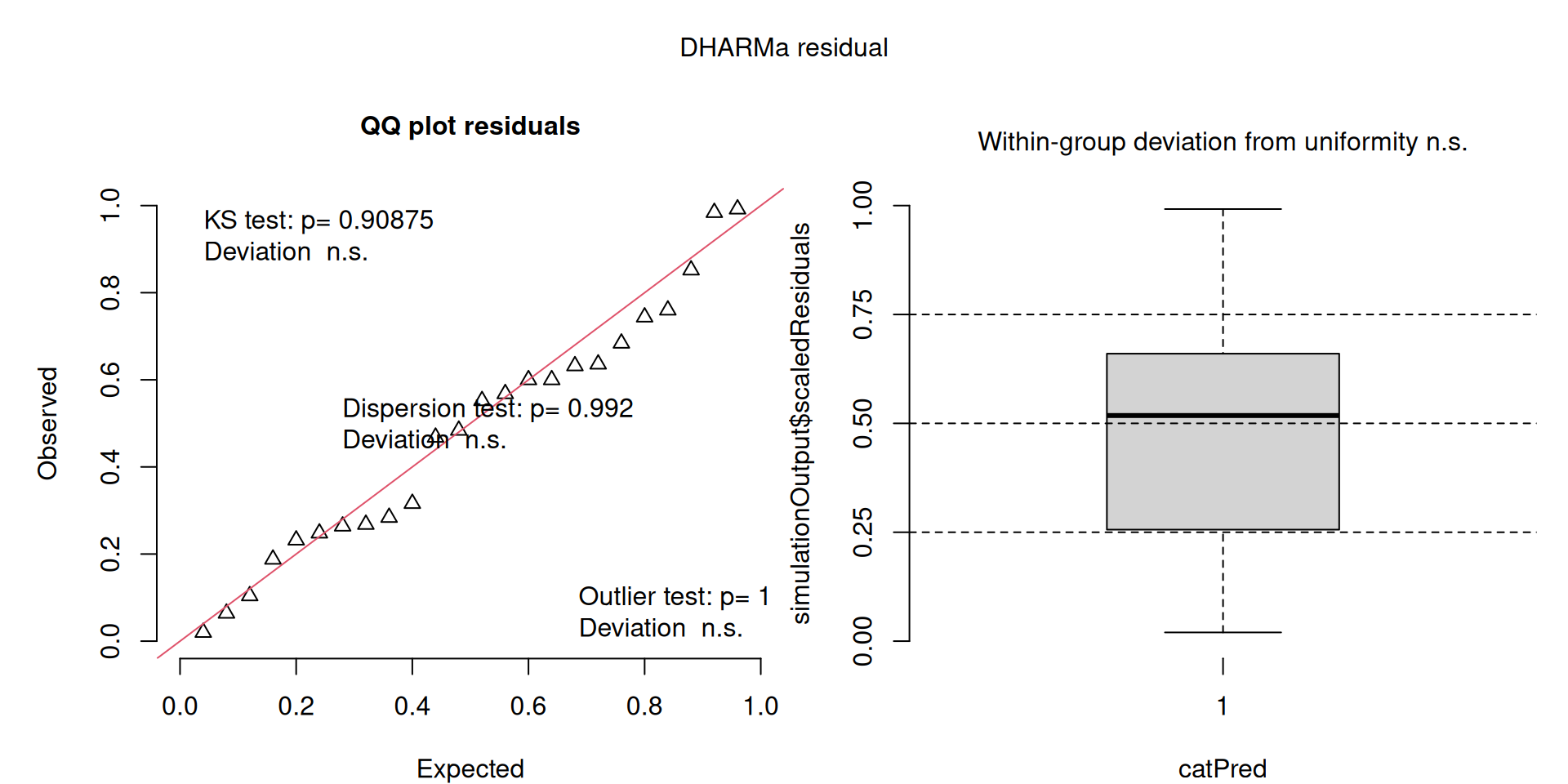
Similarly, I wouldn’t be unduly worried about the scary red line in this plot, as I don’t really find the residuals to show much pattern and there are no other problems highlighted.

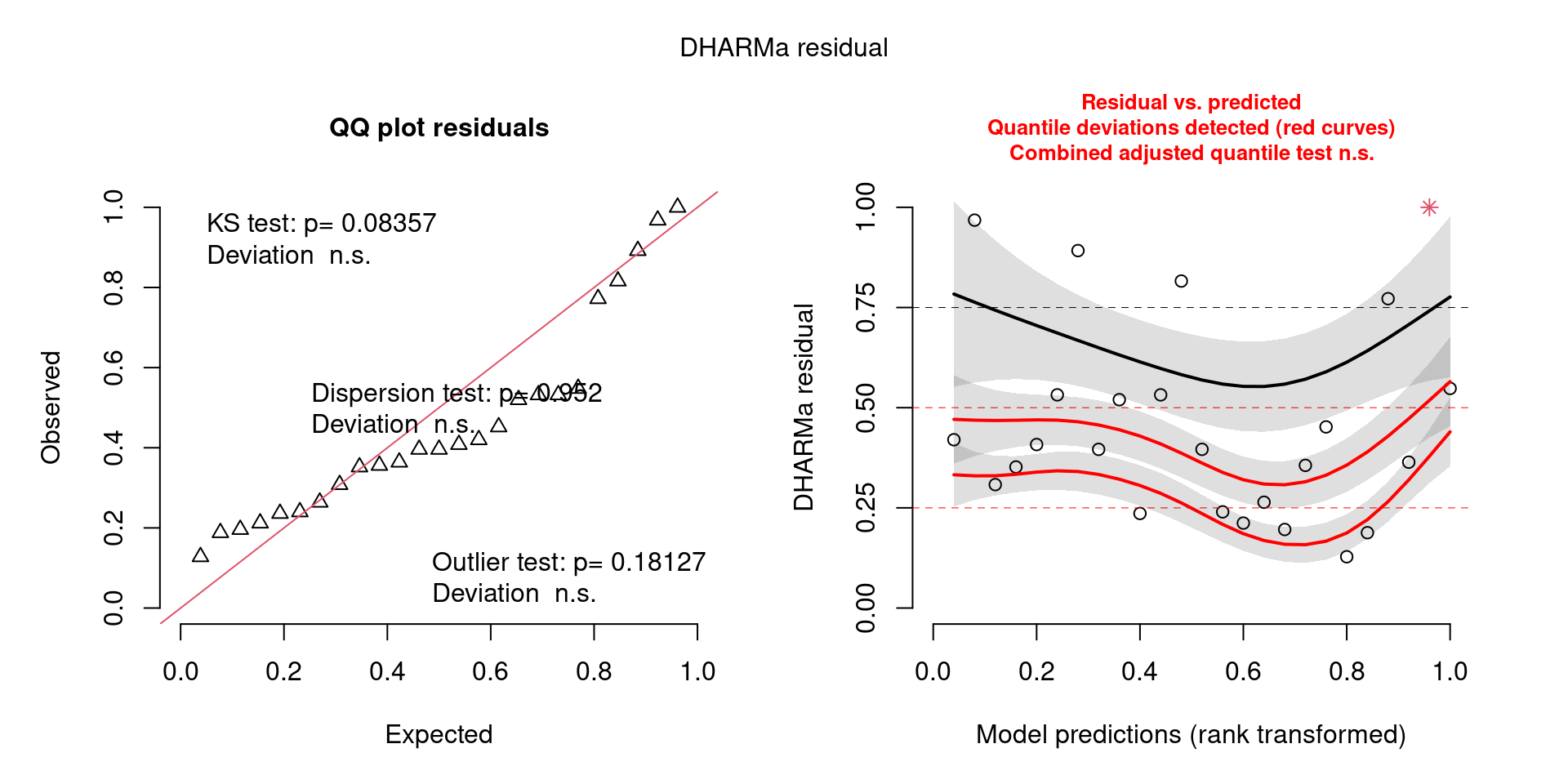
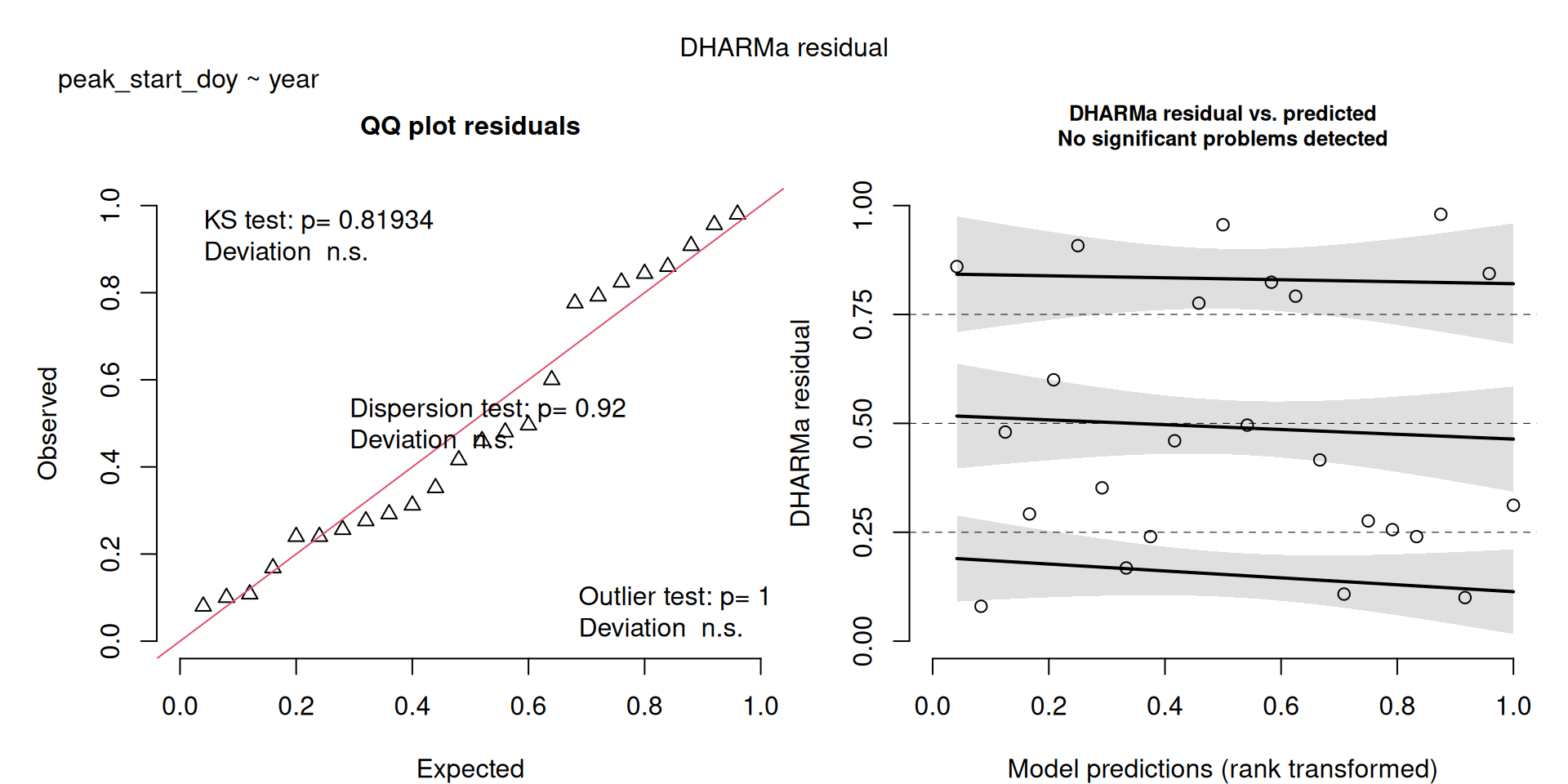
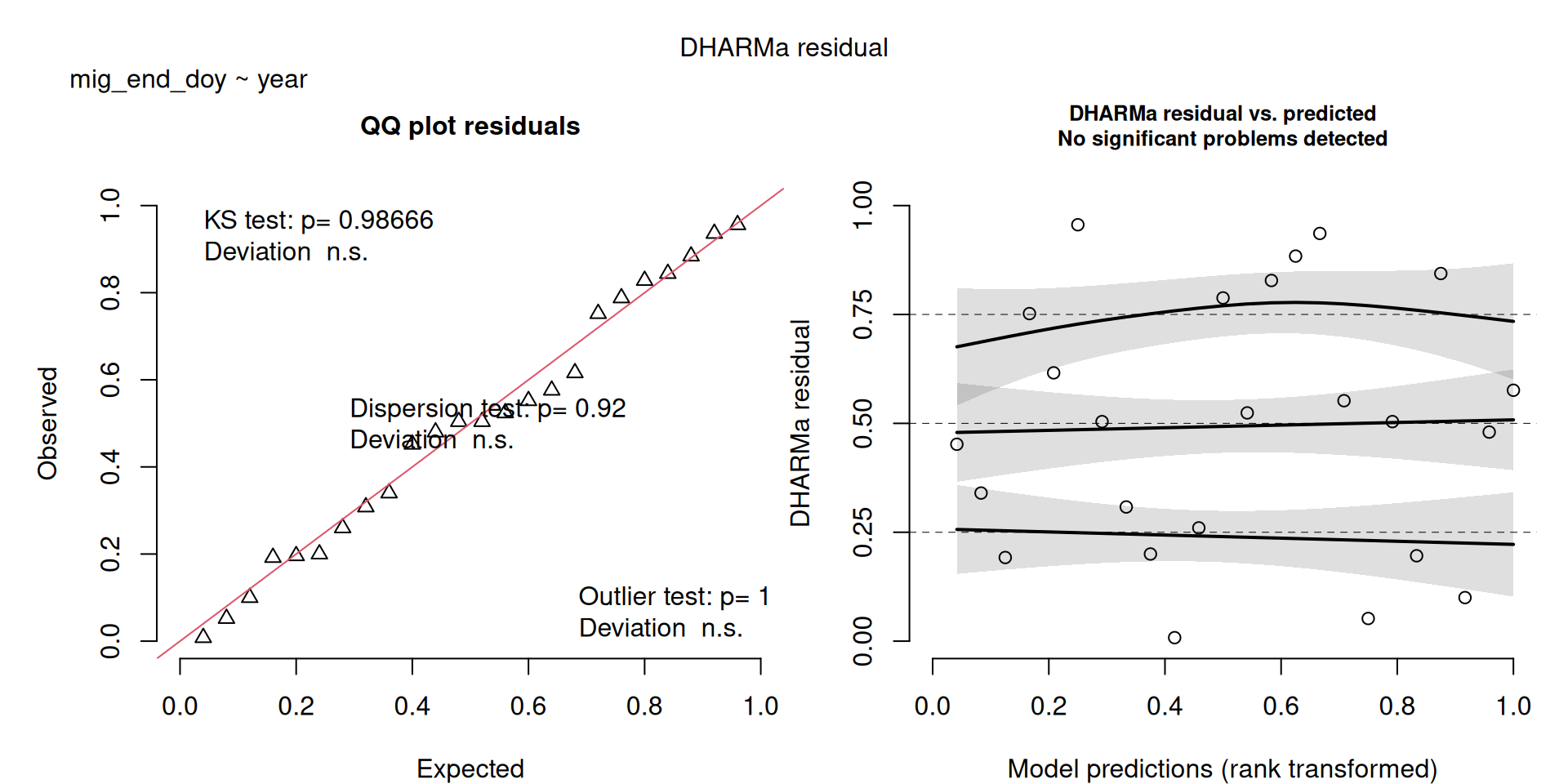
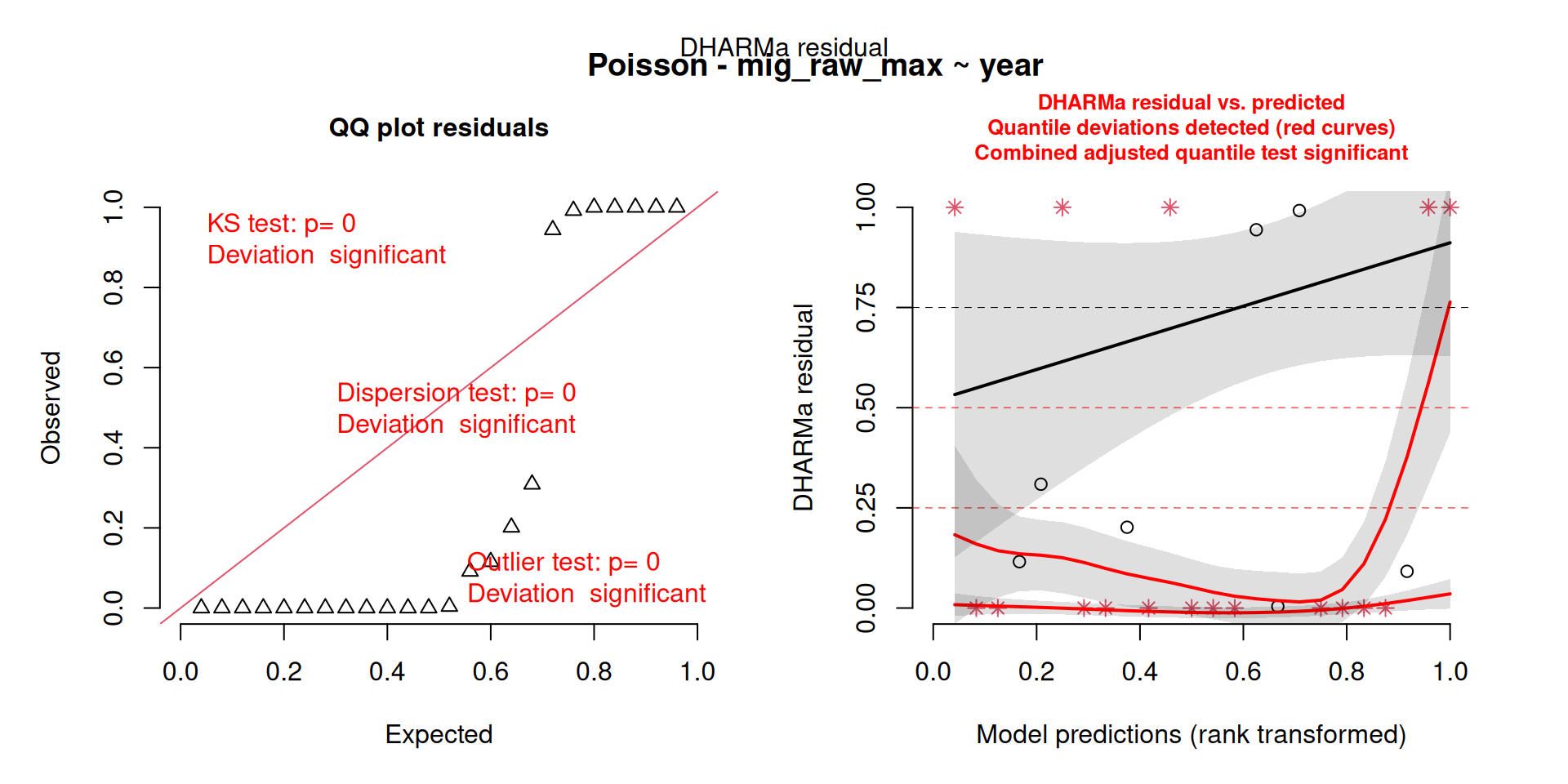
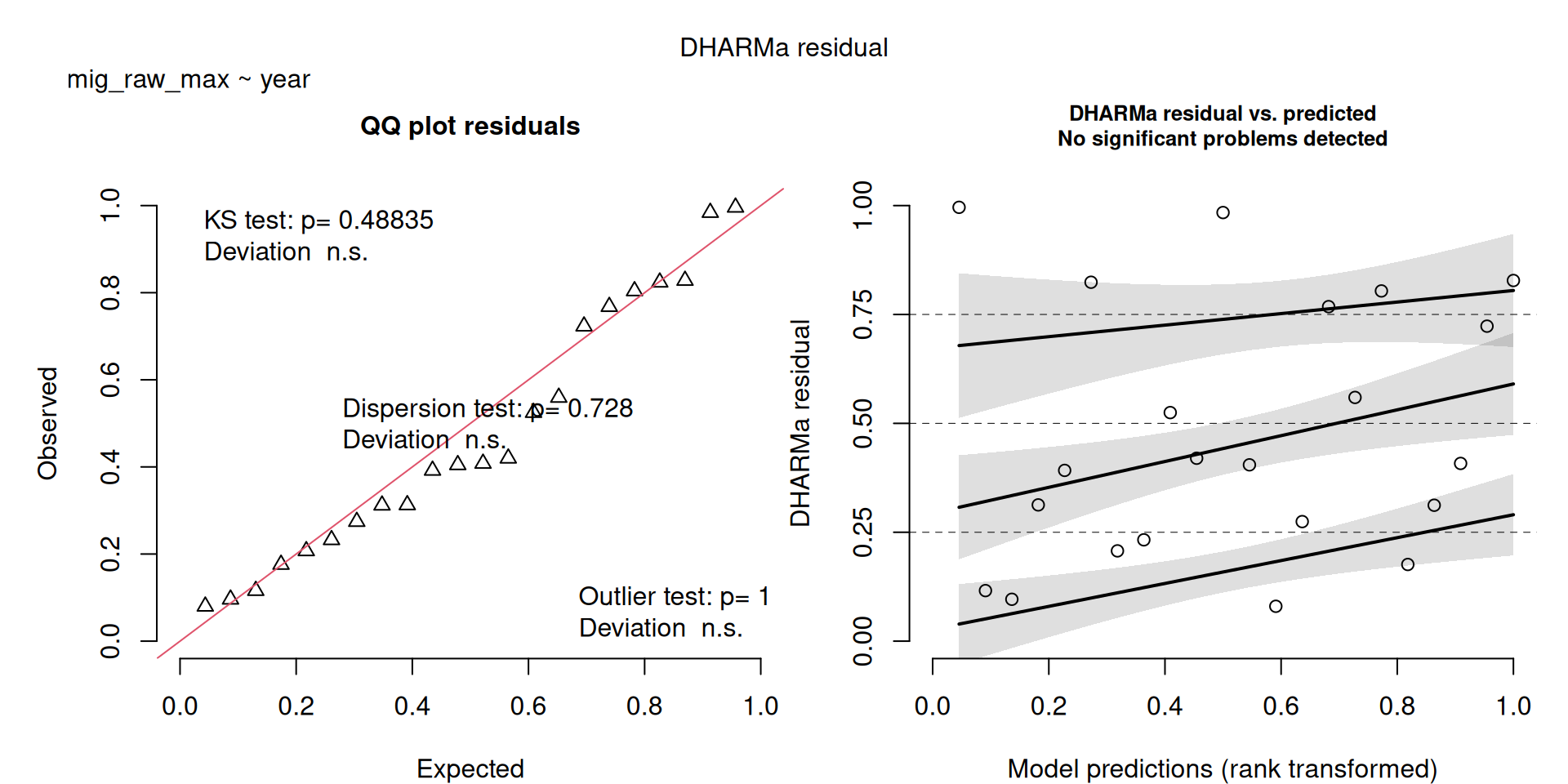
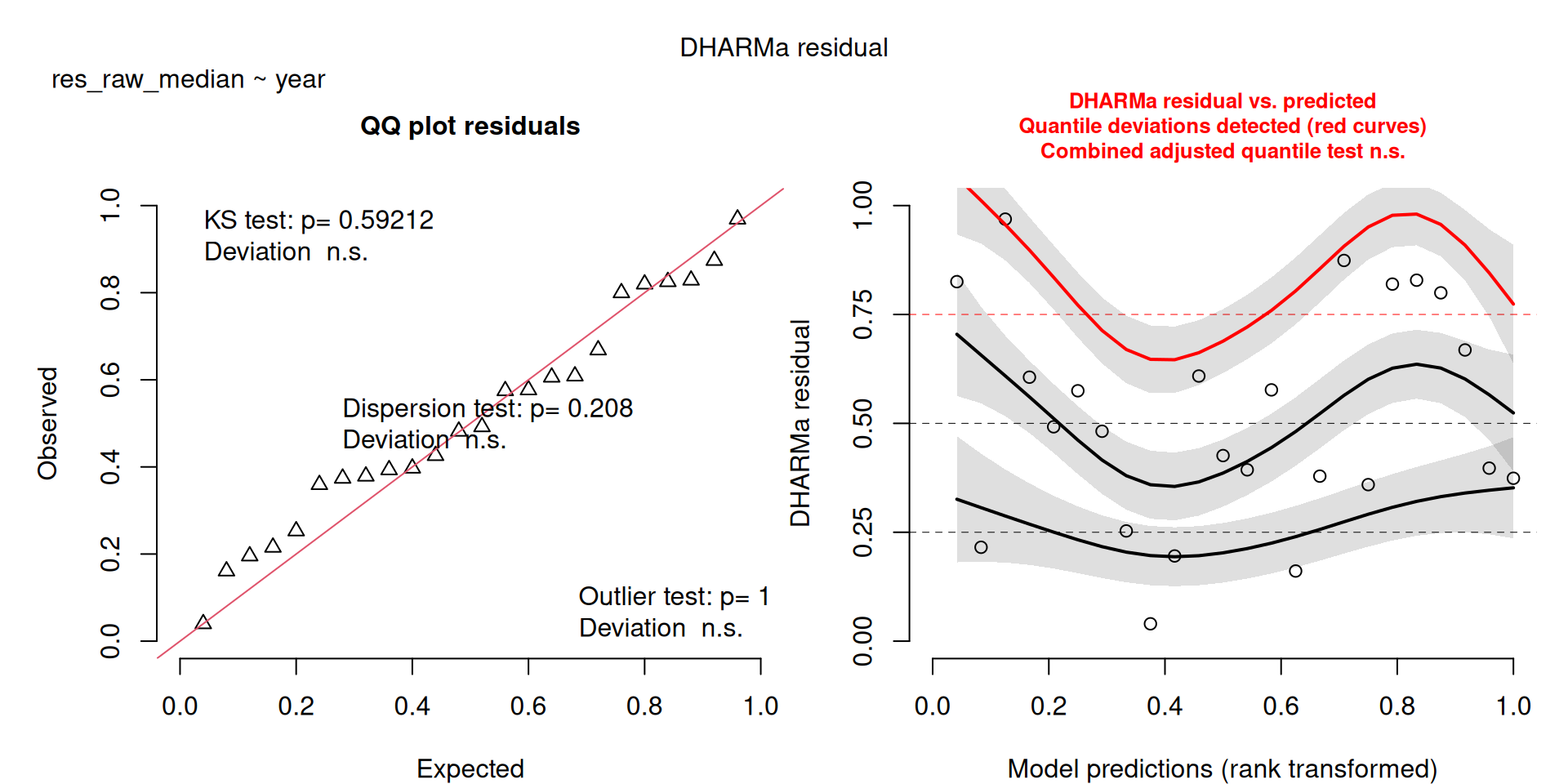
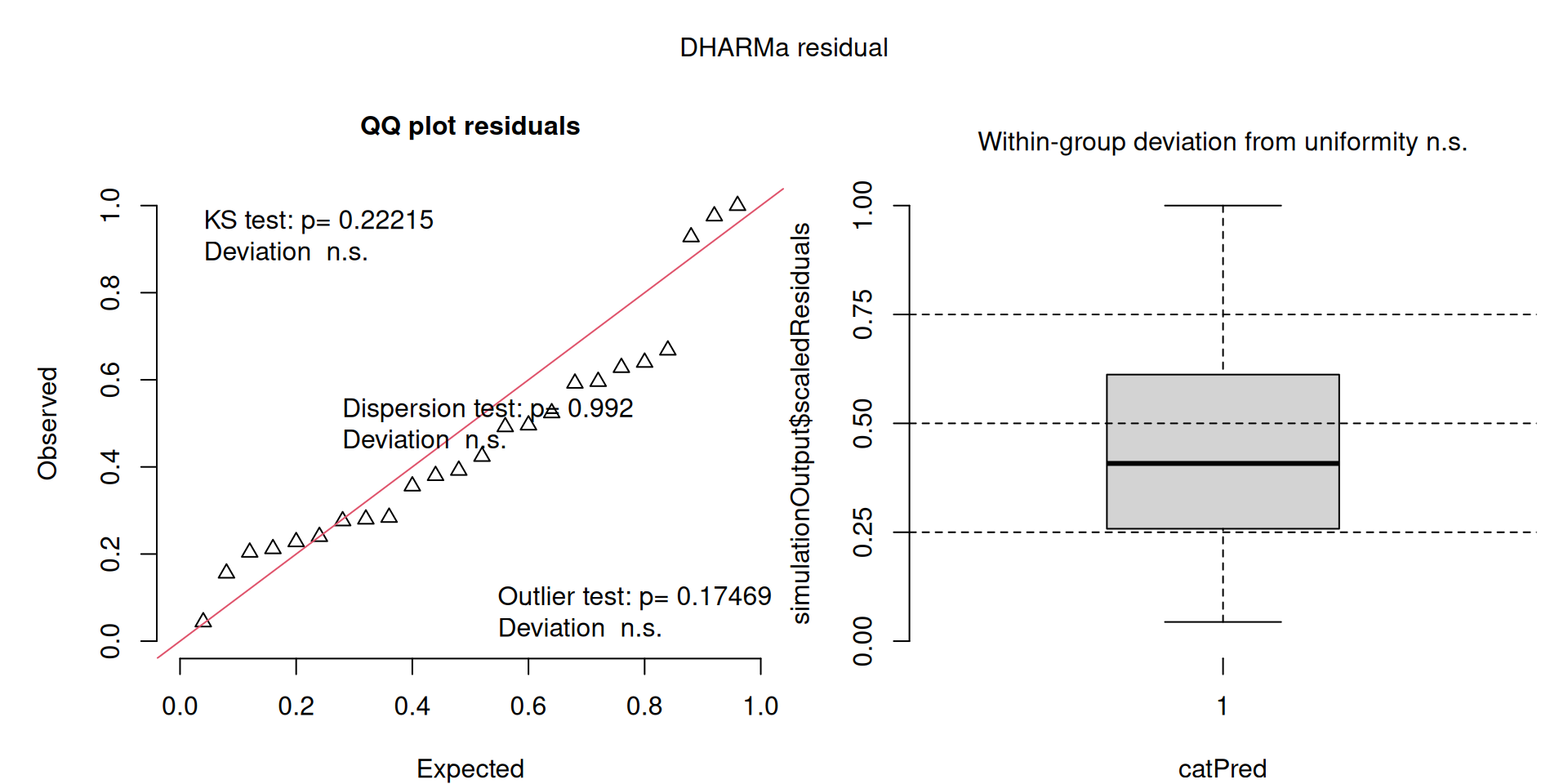
This one starts to look a bit problematic…

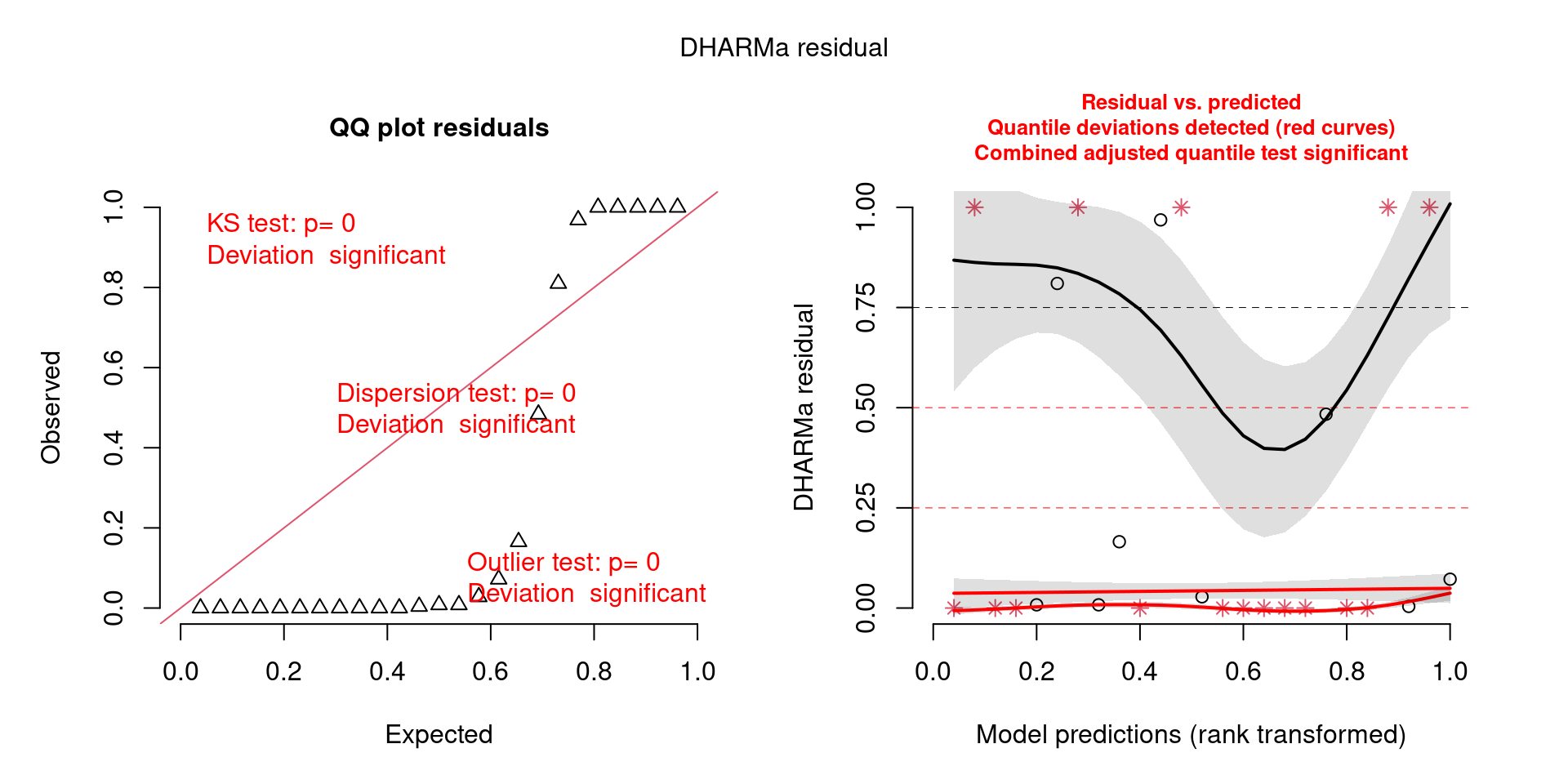
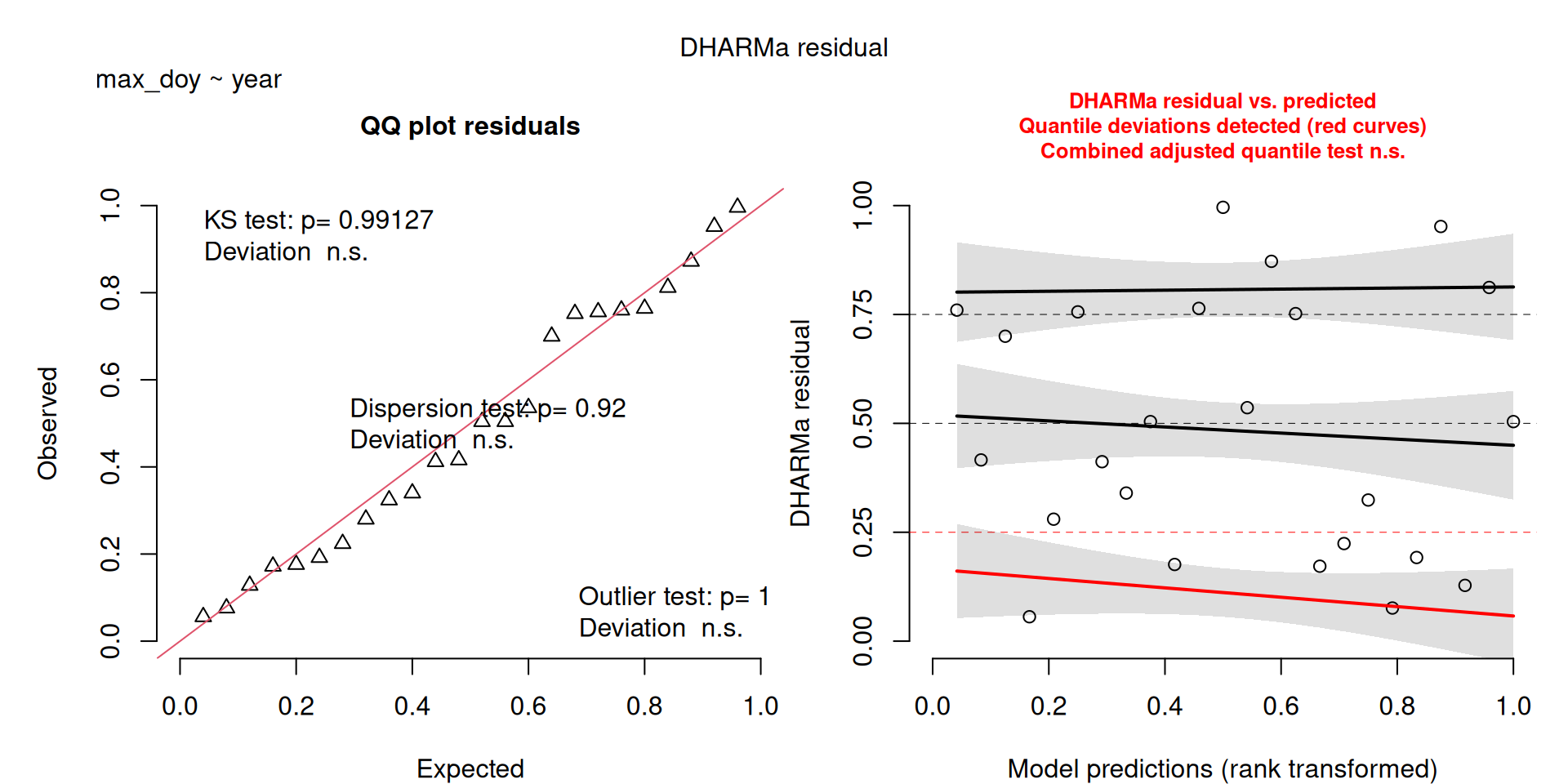
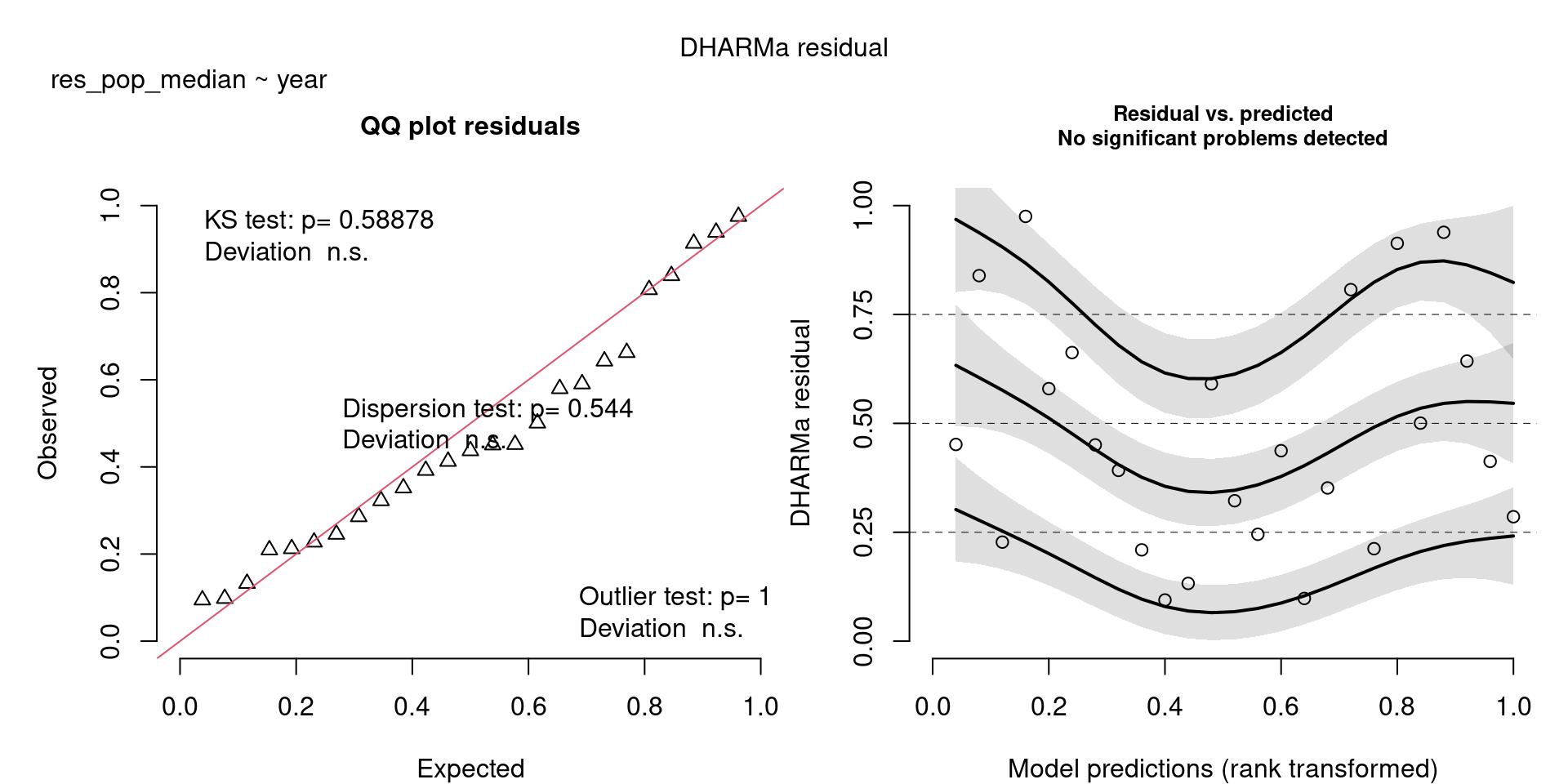
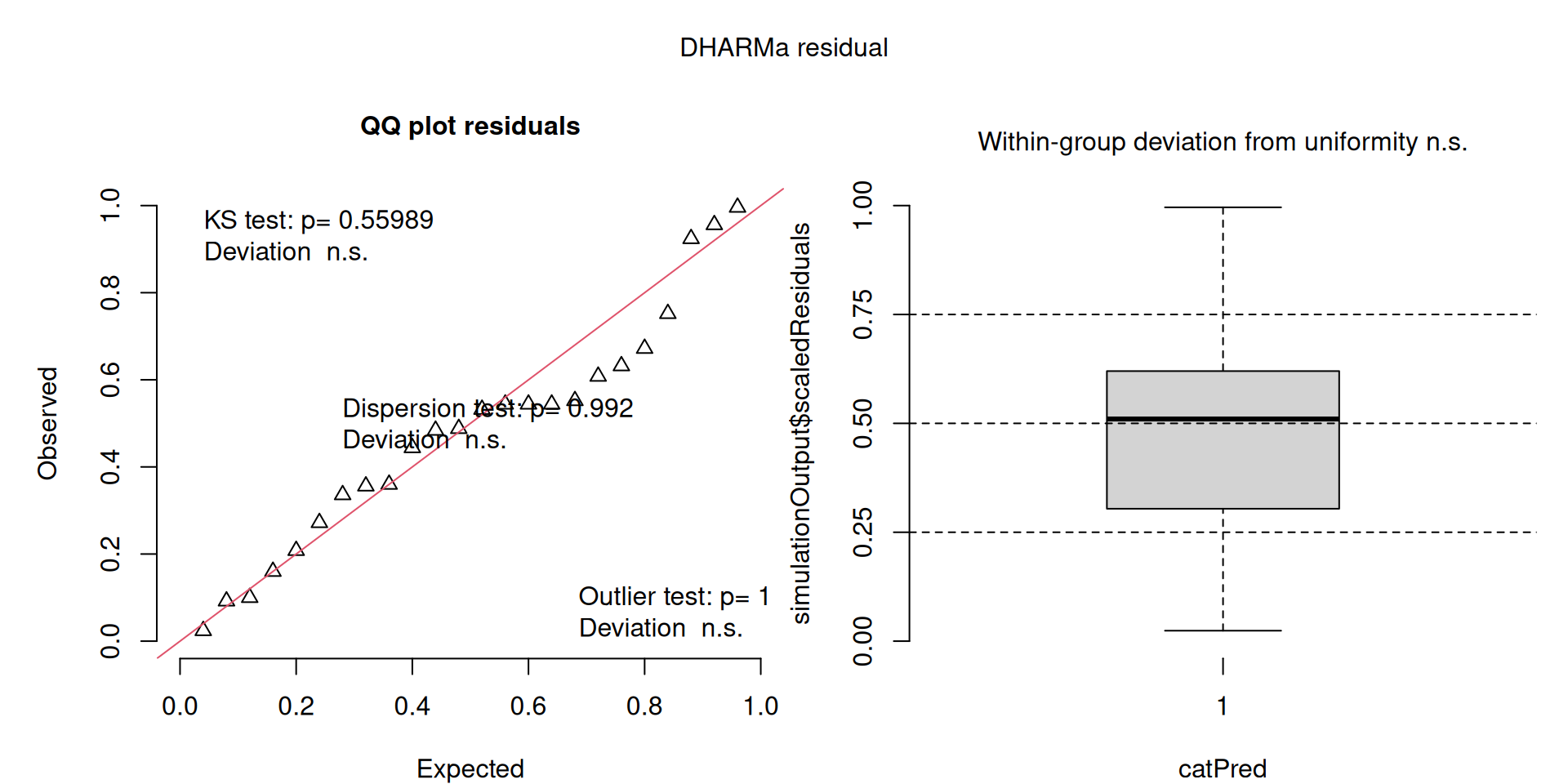
This one is awful!

Sensitivity

The DHARMa model checks will usually catch outlier problems, but out of an abundance of caution, we’ll do a quick review of any high Cook’s D values and will rerun the models without certain data points to ensure they’re still acceptable.

These sections first calculate and show the Cook’s D for all observations in each model. In these tables, values highlighted in red are more than 4/25 (a standard Cook’s D cutoff 4/sample size). These indicate potential influential data points for a particular model.

Then I run a comparison of the model before and the after removing that point.

In every case here the pattern was either strengthened or weakened by the removal, but the overall pattern did not change (no Estimate signs changed, and significance changed from sig to non-sig or vice versa).

  • Strengthened patterns showed greater Estimates and smaller P values
  • Weakened patterns showed smaller Estimates and greater P values

Tables with coefficients for both original and new model are shown, with colour intensity showing strength in the pattern.

Timing of kettle formation

When do kettles form? Has this timing changed over the years?

  • Look for changes in the DOY of the 5%, 25%, 50%, 75%, 95%, of passage as well as the DOY with the highest predicted count.
  • mig_start_doy, peak_start_doy, p50_doy, peak_end_doy, mig_end_doy, max_doy

Descriptive stats

Day of Year

Code 
v |> 
  select(contains("start_doy"), contains("50_doy"), contains("end_doy"), "max_doy") |>
  desc_stats()
measure mean sd min median max n
mig_start_doy 259.50 3.02 253 259.5 265 24
peak_start_doy 266.88 2.31 262 267.0 272 24
p50_doy 271.62 2.32 268 271.0 277 24
mig_end_doy 283.79 3.08 277 284.0 289 24
peak_end_doy 276.42 2.34 272 276.0 281 24
max_doy 271.71 2.69 266 271.0 277 24

Date

Code 
v |> 
  select(contains("start_doy"), contains("50_doy"), contains("end_doy"), "max_doy") |>
  desc_stats(units = "date")
measure mean sd min median max n
mig_start_doy Sep 17 3.02 Sep 10 Sep 17 Sep 22 24
peak_start_doy Sep 24 2.31 Sep 19 Sep 24 Sep 29 24
p50_doy Sep 29 2.32 Sep 25 Sep 28 Oct 04 24
mig_end_doy Oct 11 3.08 Oct 04 Oct 11 Oct 16 24
peak_end_doy Oct 03 2.34 Sep 29 Oct 03 Oct 08 24
max_doy Sep 29 2.69 Sep 23 Sep 28 Oct 04 24

Here we look at linear regressions of year by kettle timing dates.

m1 <- lm(mig_start_doy ~ year, data = v)
m2 <- lm(peak_start_doy ~ year, data = v)
m3 <- lm(p50_doy ~ year, data = v)
m4 <- lm(peak_end_doy ~ year, data = v)
m5 <- lm(mig_end_doy ~ year, data = v)
m6 <- lm(max_doy ~ year, data = v)

models <- list(m1, m2, m3, m4, m5, m6)

Tabulated Model Results

All show a significant increase in doy except mig_end_doy. Data saved to Data/Datasets/table_timing.csv

Code 
t1 <- get_table(models)
write_csv(t1, d)
fmt_table(t1)
term estimate std error statistic p value n
mig_start_doy ~ year (R2 = 0.26; R2-adj = 0.23)
(Intercept) −155.793 149.151 −1.045 0.308 24
year 0.206 0.074 2.784 0.011 24
peak_start_doy ~ year (R2 = 0.33; R2-adj = 0.3)
(Intercept) −91.217 108.347 −0.842 0.409 24
year 0.178 0.054 3.305 0.003 24
p50_doy ~ year (R2 = 0.28; R2-adj = 0.25)
(Intercept) −58.259 112.980 −0.516 0.611 24
year 0.164 0.056 2.920 0.008 24
peak_end_doy ~ year (R2 = 0.25; R2-adj = 0.21)
(Intercept) −37.534 116.392 −0.322 0.750 24
year 0.156 0.058 2.697 0.013 24
mig_end_doy ~ year (R2 = 0.08; R2-adj = 0.04)
(Intercept) 44.280 169.169 0.262 0.796 24
year 0.119 0.084 1.416 0.171 24
max_doy ~ year (R2 = 0.28; R2-adj = 0.25)
(Intercept) −110.936 131.392 −0.844 0.408 24
year 0.190 0.065 2.912 0.008 24

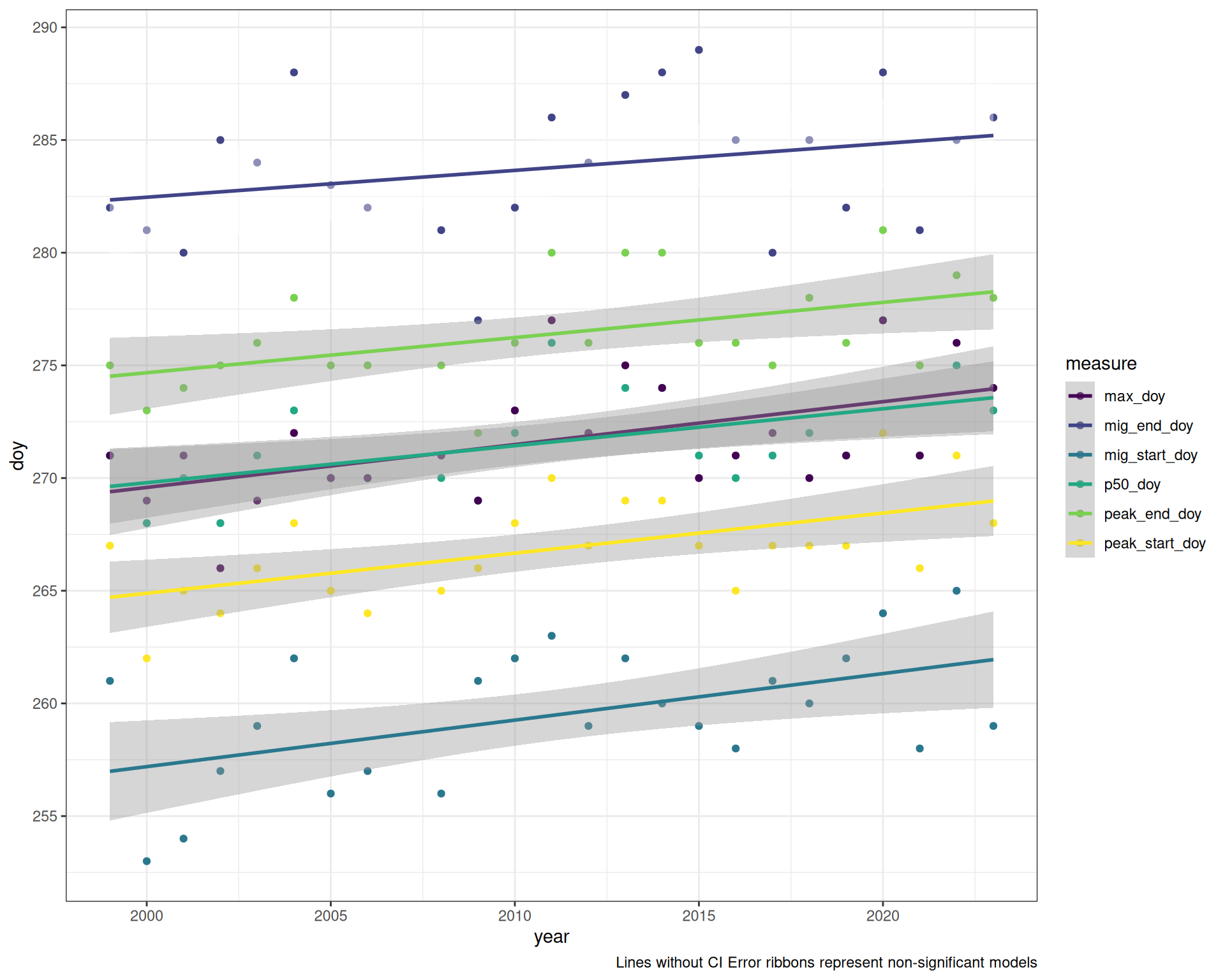
Here we look at a linear regression of year by kettle timing dates. The idea is to explore whether the interaction is significant, which would indicate that the rate of change in migration phenology differs among the seasonal points (start, start of peak, peak, end of peak, end).

We look at the effect of year and type of measurement (migration start/end, peak start/end and time of 50% passage) on date (day of year).

Code 
v1 <- select(v, ends_with("doy"), year) |>
  pivot_longer(-year, names_to = "measure", values_to = "doy")

First we look at the interaction term to see if the slopes of change among measurements are significantly different from one another.

The type III ANOVA shows no significant interaction.

Code 
m0 <- lm(doy ~ measure * year, data = v1)
car::Anova(m0, type = "III")
Anova Table (Type III tests)

Response: doy
             Sum Sq  Df F value   Pr(>F)   
(Intercept)    3.90   1  0.6954 0.405829   
measure        7.53   5  0.2681 0.929845   
year          46.46   1  8.2739 0.004691 **
measure:year   5.93   5  0.2113 0.957236   
Residuals    741.14 132                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We’ll look at a post-hoc comparison of the slopes to interpret them individually.

This is nearly identical to running the models separately, above

As with the individual models, we can see that each measure shows a significant positive slope with the exception of the End of Migration (mig_end_day).

Code 
e <- emmeans::emtrends(m0, ~ measure, var = "year") |> 
  emmeans::test()

All show a significant increase in doy except mig_end_doy. Data saved to Data/Datasets/table_timing_combined.csv

Code 
t2 <- e |> 
  mutate(
    model = "doy ~ measure * year",
    n = nrow(v)) |>
  rename(
    estimate = year.trend, 
    std_error = SE, 
    
    statistic = t.ratio, 
    p_value = p.value)

write_csv(t2, d)

fmt_table(t2) |>
  tab_header(title = "Post-hoc results") |>
  tab_footnote("Number of years in the data.", locations = cells_column_labels(n)) |>
  tab_footnote("T statistic.", locations = cells_column_labels("statistic"))
Post-hoc results
measure estimate std error df statistic1 p value n2
doy ~ measure * year
max_doy 0.190 0.066 132 2.876 0.005 24
mig_end_doy 0.119 0.066 132 1.800 0.074 24
mig_start_doy 0.206 0.066 132 3.122 0.002 24
p50_doy 0.164 0.066 132 2.480 0.014 24
peak_end_doy 0.156 0.066 132 2.360 0.020 24
peak_start_doy 0.178 0.066 132 2.692 0.008 24
1 T statistic.
2 Number of years in the data.

Note: Lines without CI ribbons are not significant

Code 
doy_figs <- v |>
  select(year, contains("doy")) |>
  pivot_longer(-year, names_to = "measure", values_to = "doy") |>
  left_join(mutate(t1, measure = str_trim(str_extract(model, "^[^~]*")), sig = p_value <= 0.05) |> 
              filter(term == "year") |>
              select(measure, sig), by = "measure")

ggplot(doy_figs, aes(x = year, y = doy, group = measure, colour = measure, fill = sig)) +
  theme_bw() +
  geom_point() +
  geom_smooth(method = "lm", se = TRUE) +
  scale_y_continuous(breaks = y_breaks) +
  scale_colour_viridis_d() +
  scale_fill_manual(values = c("TRUE" = "grey60", "FALSE" = "#FFFFFF00"), guide = "none") +
  labs(caption = "Lines without CI Error ribbons represent non-significant models")
`geom_smooth()` using formula = 'y ~ x'

The DHARMa model checks don’t highlight any particular outlier problems, but out of an abundance of caution, we’ll do a quick review of any high Cook’s D values.

Values highlighted in red are less than 4/25, a standard Cook’s D cutoff (4/sample size). These indicate potential influential data points for a particular model.

Code 
get_cooks(models) |>
  gt_cooks(width = "80%")
Cook's Distances
year mig_start_doy peak_start_doy p50_doy peak_end_doy mig_end_doy max_doy
1999 0.25 0.16 0.05 0.01 0.00 0.05
2000 0.23 0.21 0.07 0.06 0.02 0.01
2001 0.13 0.00 0.00 0.01 0.06 0.02
2002 0.00 0.03 0.07 0.00 0.04 0.19
2003 0.01 0.01 0.01 0.01 0.01 0.01
2004 0.11 0.07 0.08 0.08 0.14 0.02
2005 0.03 0.01 0.00 0.00 0.00 0.00
2006 0.01 0.04 0.01 0.00 0.01 0.00
2008 0.03 0.01 0.01 0.01 0.02 0.00
2009 0.01 0.00 0.03 0.10 0.12 0.02
2010 0.02 0.01 0.00 0.00 0.01 0.01
2011 0.04 0.06 0.11 0.07 0.01 0.12
2012 0.00 0.00 0.00 0.00 0.00 0.00
2013 0.02 0.02 0.03 0.06 0.02 0.04
2014 0.00 0.02 0.02 0.06 0.04 0.01
2015 0.01 0.00 0.01 0.01 0.07 0.03
2016 0.03 0.07 0.05 0.01 0.00 0.02
2017 0.00 0.01 0.02 0.05 0.09 0.00
2018 0.01 0.01 0.01 0.00 0.00 0.08
2019 0.01 0.02 0.05 0.03 0.04 0.05
2020 0.06 0.22 0.24 0.15 0.07 0.15
2021 0.13 0.14 0.09 0.15 0.13 0.09
2022 0.13 0.11 0.06 0.02 0.00 0.08
2023 0.13 0.03 0.01 0.00 0.01 0.00

Check influential points

Now let’s see what happens if we were to omit these years from the respective analyses.

Tables with coefficients for both original and new model are shown, with colour intensity showing strength in the pattern.

For the start of migration, if we omit 1999, the pattern is stronger, but the same, if we omit 2000, the pattern is weaker but still the same.

compare(m1, 1999)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_start_doy (Intercept) -155.793 149.151 -1.045 0.308
Drop 1999 - mig_start_doy (Intercept) -246.743 152.473 -1.618 0.121
Original - mig_start_doy year 0.206 0.074 2.784 0.011
Drop 1999 - mig_start_doy year 0.252 0.076 3.320 0.003 
compare(m1, 2000)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_start_doy (Intercept) -155.793 149.151 -1.045 0.308
Drop 2000 - mig_start_doy (Intercept) -70.361 150.113 -0.469 0.644
Original - mig_start_doy year 0.206 0.074 2.784 0.011
Drop 2000 - mig_start_doy year 0.164 0.075 2.199 0.039

For the start of peak migration

compare(m2, 2000)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_start_doy (Intercept) -91.217 108.347 -0.842 0.409
Drop 2000 - peak_start_doy (Intercept) -32.416 109.888 -0.295 0.771
Original - peak_start_doy year 0.178 0.054 3.305 0.003
Drop 2000 - peak_start_doy year 0.149 0.055 2.726 0.013 
compare(m2, 2020)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_start_doy (Intercept) -91.217 108.347 -0.842 0.409
Drop 2020 - peak_start_doy (Intercept) -36.595 104.279 -0.351 0.729
Original - peak_start_doy year 0.178 0.054 3.305 0.003
Drop 2020 - peak_start_doy year 0.151 0.052 2.908 0.008

The date of 50% passage

compare(m3, 2020)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - p50_doy (Intercept) -58.259 112.980 -0.516 0.611
Drop 2020 - p50_doy (Intercept) 2.113 107.339 0.020 0.984
Original - p50_doy year 0.164 0.056 2.920 0.008
Drop 2020 - p50_doy year 0.134 0.053 2.509 0.020

And the date of maximum counts

compare(m6, 2002)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - max_doy (Intercept) -110.936 131.392 -0.844 0.408
Drop 2002 - max_doy (Intercept) -46.968 128.776 -0.365 0.719
Original - max_doy year 0.190 0.065 2.912 0.008
Drop 2002 - max_doy year 0.159 0.064 2.477 0.022

Therefore I wouldn’t be concerned

In addition to the sensitivity check using cook’s distances, here we will conduct a more targeted exploration of some specific years.

Gaps around the peak

First, we consider removing 2011, 2013 as they have sampling gaps around the peak of migration

y <- c(2011, 2013)
m1a <- update(m1, data = filter(v, !year %in% y))
m2a <- update(m2, data = filter(v, !year %in% y))
m3a <- update(m3, data = filter(v, !year %in% y))
m4a <- update(m4, data = filter(v, !year %in% y))
m5a <- update(m5, data = filter(v, !year %in% y))
m6a <- update(m6, data = filter(v, !year %in% y))

models_a <- list(m1a, m2a, m3a, m4a, m5a, m6a)

Comparing the summary tables shows only superficial differences. If anything, it looks like removing these ‘gappy’ years only strengthens the existing patterns. Those which are significant are slightly more so, and the slopes are slightly greater.

Data saved to Data/Datasets/table_supplemental.csv

Original

Code 
fmt_summary(models, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_start_doy ~ year year 0.206 0.074 2.784 0.011
peak_start_doy ~ year year 0.178 0.054 3.305 0.003
p50_doy ~ year year 0.164 0.056 2.920 0.008
peak_end_doy ~ year year 0.156 0.058 2.697 0.013
mig_end_doy ~ year year 0.119 0.084 1.416 0.171
max_doy ~ year year 0.190 0.065 2.912 0.008
Code 
to <- get_table(models) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "original")
write_csv(to, d)

Years removed

Code 
fmt_summary(models_a, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_start_doy ~ year year 0.204 0.073 2.784 0.011
peak_start_doy ~ year year 0.176 0.051 3.416 0.003
p50_doy ~ year year 0.161 0.050 3.237 0.004
peak_end_doy ~ year year 0.151 0.052 2.928 0.008
mig_end_doy ~ year year 0.115 0.085 1.352 0.192
max_doy ~ year year 0.186 0.056 3.324 0.003
Code 
ta <- get_table(models_a) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "gaps_removed")
write_csv(ta, d, append = TRUE)

Missing the end of migration

Second, we consider removing 2001, 2006, 2023 as they were three years where it looks like sampling ended earlier than the end of migration.

y <- c(2001, 2006, 2023)
m1b <- update(m1, data = filter(v, !year %in% y))
m2b <- update(m2, data = filter(v, !year %in% y))
m3b <- update(m3, data = filter(v, !year %in% y))
m4b <- update(m4, data = filter(v, !year %in% y))
m5b <- update(m5, data = filter(v, !year %in% y))
m6b <- update(m6, data = filter(v, !year %in% y))

models_b <- list(m1b, m2b, m3b, m4b, m5b, m6b)

Removing these years from the analyses, reduced the strength of the patterns, but not by much. Further, there were few changes to the magnitude of the slopes.

Data saved to Data/Datasets/table_supplemental.csv

Original

Code 
fmt_summary(models, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_start_doy ~ year year 0.206 0.074 2.784 0.011
peak_start_doy ~ year year 0.178 0.054 3.305 0.003
p50_doy ~ year year 0.164 0.056 2.920 0.008
peak_end_doy ~ year year 0.156 0.058 2.697 0.013
mig_end_doy ~ year year 0.119 0.084 1.416 0.171
max_doy ~ year year 0.190 0.065 2.912 0.008

Years removed

Code 
fmt_summary(models_b, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_start_doy ~ year year 0.198 0.082 2.410 0.026
peak_start_doy ~ year year 0.178 0.063 2.825 0.011
p50_doy ~ year year 0.167 0.068 2.467 0.023
peak_end_doy ~ year year 0.147 0.070 2.119 0.048
mig_end_doy ~ year year 0.077 0.099 0.781 0.445
max_doy ~ year year 0.198 0.078 2.530 0.020
Code 
tb <- get_table(models_b) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "end_removed")
write_csv(tb, d, append = TRUE)

Remove all problematic years

Out of curiosity, let’s try removing all 5 years. This reduces our data from 25 to 19 samples, so is a substantial change and we may see non-significant results merely because we have removed too many samples.

y <- c(2011, 2013, 2001, 2006, 2023)
m1c <- update(m1, data = filter(v, !year %in% y))
m2c <- update(m2, data = filter(v, !year %in% y))
m3c <- update(m3, data = filter(v, !year %in% y))
m4c <- update(m4, data = filter(v, !year %in% y))
m5c <- update(m5, data = filter(v, !year %in% y))
m6c <- update(m6, data = filter(v, !year %in% y))

models_c <- list(m1c, m2c, m3c, m4c, m5c, m6c)

Removing these years from the analyses, reduced the strength of the patterns, but not by much. Further, there are few changes to the magnitude of the slopes.

Data saved to Data/Datasets/table_supplemental.csv

Original

Code 
fmt_summary(models, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_start_doy ~ year year 0.206 0.074 2.784 0.011
peak_start_doy ~ year year 0.178 0.054 3.305 0.003
p50_doy ~ year year 0.164 0.056 2.920 0.008
peak_end_doy ~ year year 0.156 0.058 2.697 0.013
mig_end_doy ~ year year 0.119 0.084 1.416 0.171
max_doy ~ year year 0.190 0.065 2.912 0.008

Years removed

Code 
fmt_summary(models_c, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_start_doy ~ year year 0.196 0.082 2.387 0.029
peak_start_doy ~ year year 0.176 0.061 2.893 0.010
p50_doy ~ year year 0.165 0.061 2.715 0.015
peak_end_doy ~ year year 0.143 0.063 2.270 0.036
mig_end_doy ~ year year 0.073 0.101 0.722 0.480
max_doy ~ year year 0.195 0.067 2.901 0.010
Code 
tc <- get_table(models_c) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "all_removed")
write_csv(tc, d, append = TRUE)

Conclusions

I do not believe that these potentially problematic sampling years are driving the patterns we see in this data.

At worst, by removing these years we increase the error around a slope. But the magnitudes of the slopes do not change very much and even the significance is only ever reduced only a little.

Code 
models <- append(list(m0), models)
map(models, summary)
[[1]]

Call:
lm(formula = doy ~ measure * year, data = v1)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.5336 -1.5933 -0.3033  1.6795  5.3234 

Coefficients:
                             Estimate Std. Error t value Pr(>|t|)   
(Intercept)                -110.93571  133.02821  -0.834  0.40583   
measuremig_end_doy          155.21571  188.13030   0.825  0.41084   
measuremig_start_doy        -44.85714  188.13030  -0.238  0.81191   
measurep50_doy               52.67714  188.13030   0.280  0.77991   
measurepeak_end_doy          73.40143  188.13030   0.390  0.69705   
measurepeak_start_doy        19.71857  188.13030   0.105  0.91668   
year                          0.19026    0.06614   2.876  0.00469 **
measuremig_end_doy:year      -0.07117    0.09354  -0.761  0.44812   
measuremig_start_doy:year     0.01623    0.09354   0.174  0.86249   
measurep50_doy:year          -0.02623    0.09354  -0.280  0.77957   
measurepeak_end_doy:year     -0.03416    0.09354  -0.365  0.71559   
measurepeak_start_doy:year   -0.01221    0.09354  -0.131  0.89637   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.37 on 132 degrees of freedom
Multiple R-squared:  0.9189,    Adjusted R-squared:  0.9122 
F-statistic:   136 on 11 and 132 DF,  p-value: < 2.2e-16


[[2]]

Call:
lm(formula = mig_start_doy ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.1942 -2.2945 -0.3461  2.2601  4.0123 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept) -155.79286  149.15112  -1.045   0.3076  
year           0.20649    0.07416   2.784   0.0108 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.657 on 22 degrees of freedom
Multiple R-squared:  0.2606,    Adjusted R-squared:  0.227 
F-statistic: 7.753 on 1 and 22 DF,  p-value: 0.01081


[[3]]

Call:
lm(formula = peak_start_doy ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.8868 -1.2496 -0.5234  1.6650  3.5522 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) -91.21714  108.34732  -0.842  0.40891   
year          0.17805    0.05387   3.305  0.00322 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.93 on 22 degrees of freedom
Multiple R-squared:  0.3318,    Adjusted R-squared:  0.3014 
F-statistic: 10.92 on 1 and 22 DF,  p-value: 0.003223


[[4]]

Call:
lm(formula = p50_doy ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.4178 -1.6347 -0.5897  1.4275  4.4023 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) -58.25857  112.98029  -0.516  0.61124   
year          0.16403    0.05618   2.920  0.00794 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.012 on 22 degrees of freedom
Multiple R-squared:  0.2793,    Adjusted R-squared:  0.2465 
F-statistic: 8.526 on 1 and 22 DF,  p-value: 0.007935


[[5]]

Call:
lm(formula = peak_end_doy ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.0784 -1.0541 -0.3590  0.8667  3.6094 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)  
(Intercept) -37.53429  116.39244  -0.322   0.7501  
year          0.15610    0.05787   2.697   0.0132 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.073 on 22 degrees of freedom
Multiple R-squared:  0.2485,    Adjusted R-squared:  0.2144 
F-statistic: 7.276 on 1 and 22 DF,  p-value: 0.01316


[[6]]

Call:
lm(formula = mig_end_doy ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.5336 -1.8432  0.0259  2.2461  5.0618 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept)  44.28000  169.16915   0.262    0.796
year          0.11909    0.08411   1.416    0.171

Residual standard error: 3.013 on 22 degrees of freedom
Multiple R-squared:  0.08351,   Adjusted R-squared:  0.04185 
F-statistic: 2.005 on 1 and 22 DF,  p-value: 0.1708


[[7]]

Call:
lm(formula = max_doy ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.9643 -1.7706 -0.3205  1.6187  5.3234 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept) -110.93571  131.39209  -0.844  0.40758   
year           0.19026    0.06533   2.912  0.00808 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.34 on 22 degrees of freedom
Multiple R-squared:  0.2782,    Adjusted R-squared:  0.2454 
F-statistic: 8.481 on 1 and 22 DF,  p-value: 0.008075
Code 
model_check_figs(models)

Duration of migration

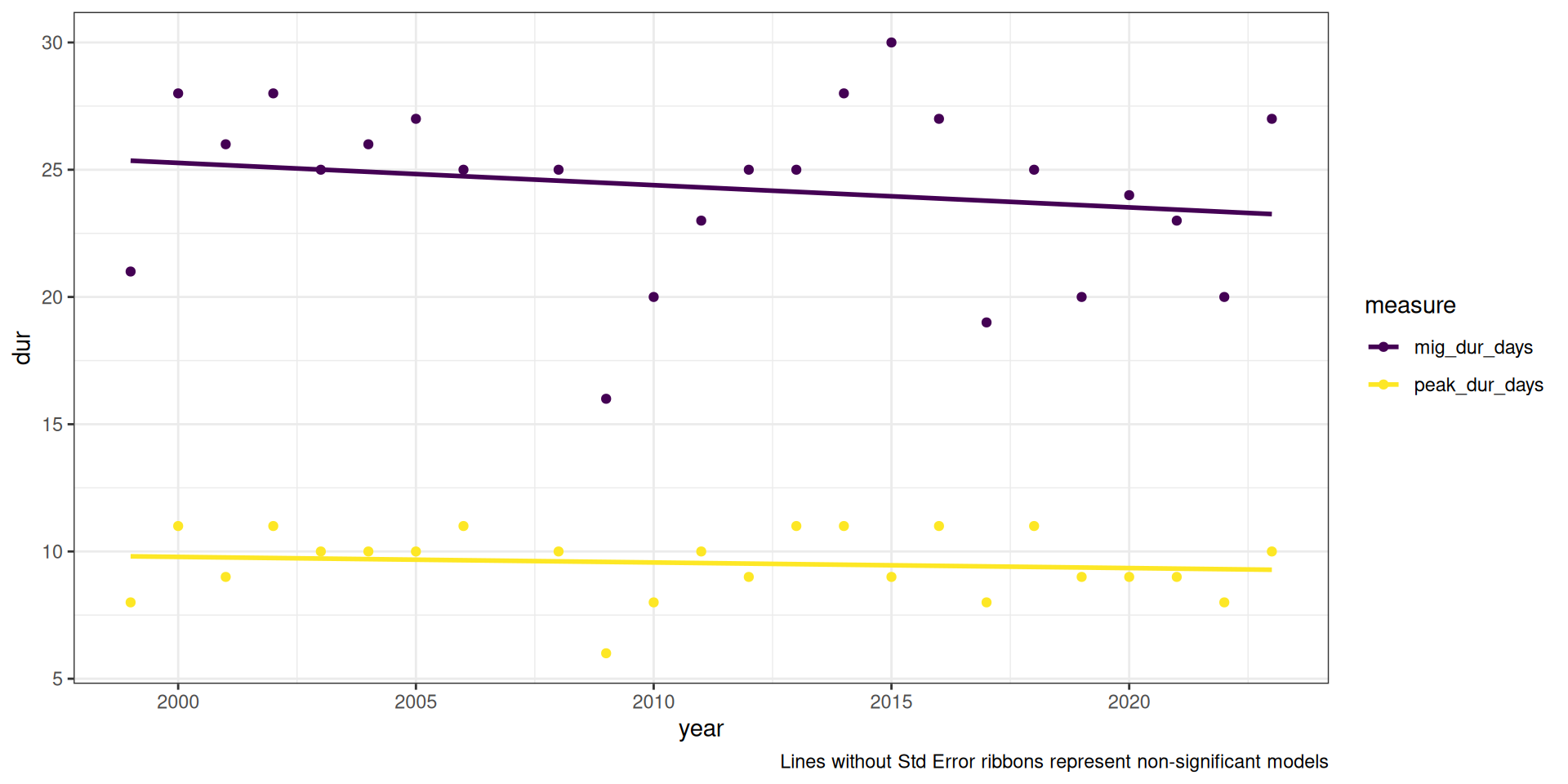
How long is migration? Has it changed in length?

  • Look for changes in the number of days over which migration and peak migration occur
  • mig_dur_days, peak_dur_days

Descriptive stats

Code 
v |> 
  select(contains("dur")) |>
  desc_stats()
measure mean sd min median max n
mig_dur_days 24.29 3.43 16 25 30 24
peak_dur_days 9.54 1.32 6 10 11 24 
m1 <- lm(mig_dur_days ~ year, data = v)
m2 <- lm(peak_dur_days ~ year, data = v)

models <- list(m1, m2)

Tabulated Results

No significant results

Code 
t <- get_table(models)
write_csv(t, "Data/Datasets/table_duration.csv")
fmt_table(t)
term estimate std error statistic p value n
mig_dur_days ~ year (R2 = 0.04; R2-adj = -0.01)
(Intercept) 200.073 193.428 1.034 0.312 24
year −0.087 0.096 −0.909 0.373 24
peak_dur_days ~ year (R2 = 0.02; R2-adj = -0.03)
(Intercept) 53.683 75.074 0.715 0.482 24
year −0.022 0.037 −0.588 0.563 24

Note: Lines without Std Error ribbons are not significant

Code 
dur_figs <- v |>
  select(year, contains("dur")) |>
  pivot_longer(-year, names_to = "measure", values_to = "dur")

ggplot(dur_figs, aes(x = year, y = dur, group = measure, colour = measure)) +
  theme_bw() +
  geom_point() +
  stat_smooth(method = "lm", se = FALSE) +
  #scale_y_continuous(breaks = y_breaks) +
  scale_colour_viridis_d()+
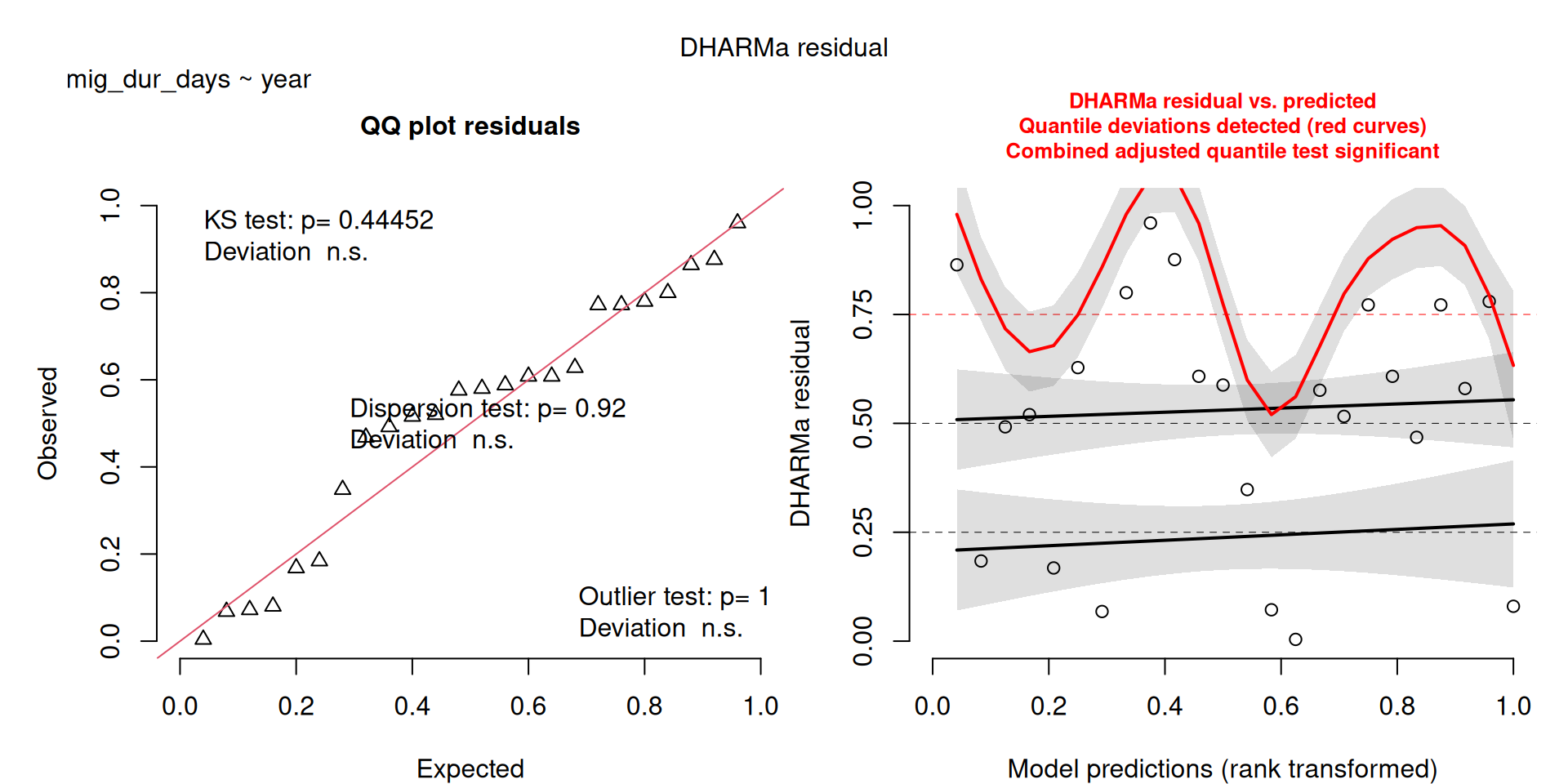
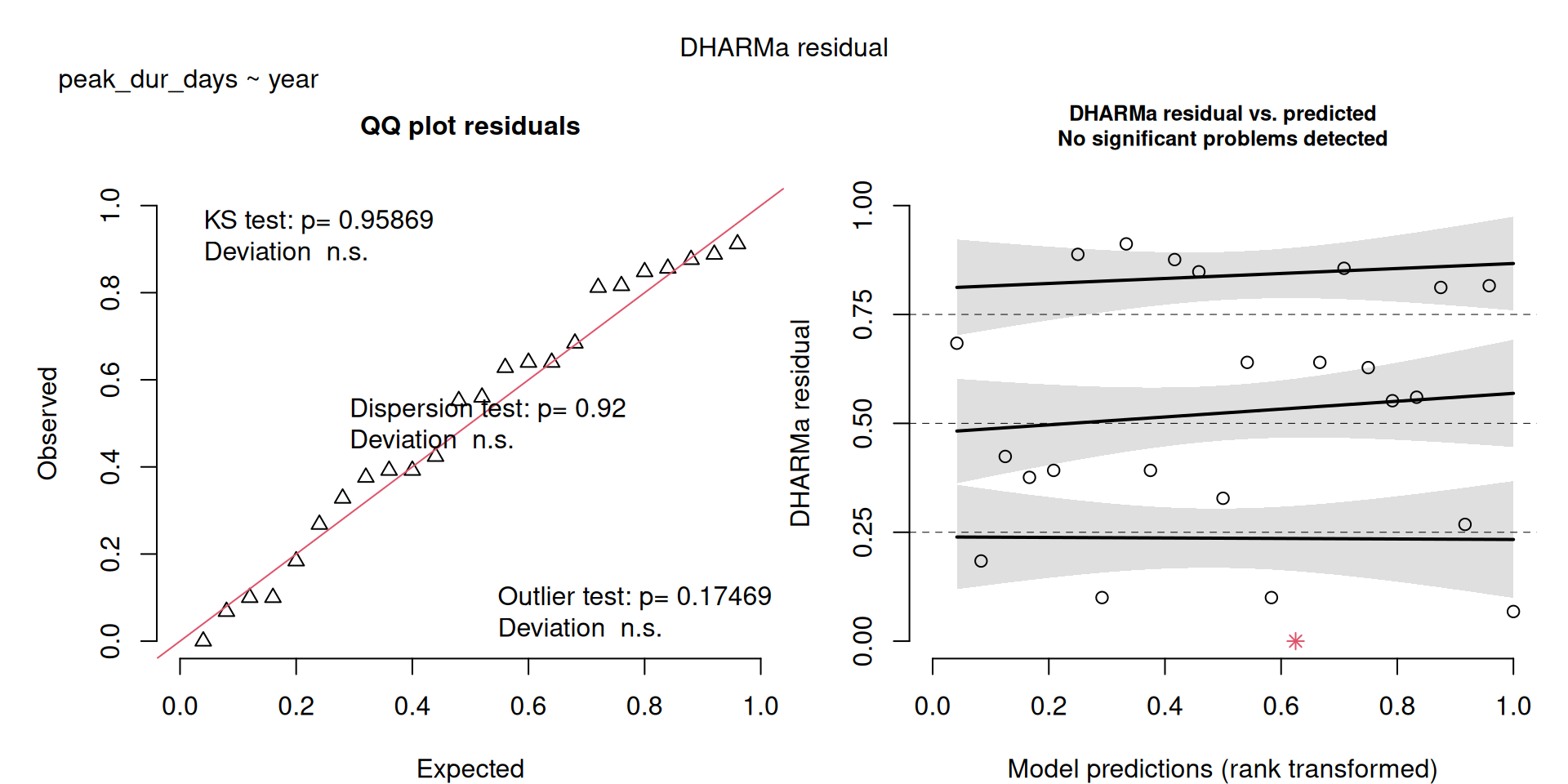
  labs(caption = "Lines without Std Error ribbons represent non-significant models")
`geom_smooth()` using formula = 'y ~ x'

Some pattern to the upper quandrant residuals, but I think the more reflects what we’re seeing, that year is a poor predictor of migration duration.

Code 
model_check_figs(models)

The DHARMa model checks don’t highlight any particular outlier problems, but out of an abundance of caution, we’ll do a quick review of any high Cook’s D values.

Values highlighted in red are less than 4/25, a standard Cook’s D cutoff (4/sample size). These indicate potential influential data points for a particular model.

Code 
get_cooks(models) |>
  gt_cooks()
Cook's Distances
year mig_dur_days peak_dur_days
1999 0.18 0.20
2000 0.06 0.08
2001 0.00 0.03
2002 0.05 0.06
2003 0.00 0.00
2004 0.00 0.00
2005 0.02 0.00
2006 0.00 0.04
2008 0.00 0.00
2009 0.15 0.18
2010 0.04 0.03
2011 0.00 0.00
2012 0.00 0.00
2013 0.00 0.03
2014 0.03 0.03
2015 0.09 0.00
2016 0.03 0.05
2017 0.08 0.04
2018 0.01 0.07
2019 0.06 0.00
2020 0.00 0.00
2021 0.00 0.00
2022 0.08 0.08
2023 0.12 0.03

Check influential points

Now let’s see what happens if we were to omit these years from the respective analyses.

Tables with coefficients for both original and new model are shown, with colour intensity showing strength in the pattern.

For the number of days in peak migration, if we omit 1999, the pattern is stronger, but the same (i.e. not significant), we see the same for the number of days in peak migration for 1999 and 2009.

compare(m1, 1999)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_dur_days (Intercept) 200.073 193.428 1.034 0.312
Drop 1999 - mig_dur_days (Intercept) 298.792 201.845 1.480 0.154
Original - mig_dur_days year -0.087 0.096 -0.909 0.373
Drop 1999 - mig_dur_days year -0.136 0.100 -1.359 0.188 
compare(m2, 1999)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_dur_days (Intercept) 53.683 75.074 0.715 0.482
Drop 1999 - peak_dur_days (Intercept) 94.682 77.803 1.217 0.237
Original - peak_dur_days year -0.022 0.037 -0.588 0.563
Drop 1999 - peak_dur_days year -0.042 0.039 -1.093 0.287 
compare(m2, 2009)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_dur_days (Intercept) 53.683 75.074 0.715 0.482
Drop 2009 - peak_dur_days (Intercept) 66.605 62.405 1.067 0.298
Original - peak_dur_days year -0.022 0.037 -0.588 0.563
Drop 2009 - peak_dur_days year -0.028 0.031 -0.912 0.372

Therefore I wouldn’t be concerned

In addition to the sensitivity check using cook’s distances, here we will conduct a more targeted exploration of some specific years.

Gaps around the peak

First, we consider removing 2011, 2013 as they have sampling gaps around the peak of migration

y <- c(2011, 2013)
m1a <- update(m1, data = filter(v, !year %in% y))
m2a <- update(m2, data = filter(v, !year %in% y))
models_a <- list(m1a, m2a)

Comparing the summary tables shows only superficial differences.

Data saved to Data/Datasets/table_supplemental.csv

Original

fmt_summary(models, intercept = FALSE)
to <- get_table(models) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "original")
write_csv(to, d, append = TRUE)
model Parameter Estimate Std. Error T P
mig_dur_days ~ year year −0.087 0.096 −0.909 0.373
peak_dur_days ~ year year −0.022 0.037 −0.588 0.563

Years removed

fmt_summary(models_a, intercept = FALSE)
ta <- get_table(models_a) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "gaps_removed")
write_csv(ta, d, append = TRUE)
model Parameter Estimate Std. Error T P
mig_dur_days ~ year year −0.089 0.101 −0.883 0.388
peak_dur_days ~ year year −0.024 0.038 −0.638 0.531

Missing the end of migration

Second, we consider removing 2001, 2006, 2023 as they were three years where it looks like sampling ended earlier than the end of migration.

y <- c(2001, 2006, 2023)
m1b <- update(m1, data = filter(v, !year %in% y))
m2b <- update(m2, data = filter(v, !year %in% y))
models_b <- list(m1b, m2b)

Comparing the summary tables shows only superficial differences.

Data saved to Data/Datasets/table_supplemental.csv

Original

fmt_summary(models, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_dur_days ~ year year −0.087 0.096 −0.909 0.373
peak_dur_days ~ year year −0.022 0.037 −0.588 0.563

Years removed

fmt_summary(models_b, intercept = FALSE)
tb <- get_table(models_b) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "end_removed")
write_csv(tb, d, append = TRUE)
model Parameter Estimate Std. Error T P
mig_dur_days ~ year year −0.121 0.113 −1.072 0.297
peak_dur_days ~ year year −0.031 0.043 −0.713 0.485

Remove all problematic years

Out of curiosity, let’s try removing all 5 years. This reduces our data from 25 to 19 samples, so is a substantial change and we may see non-significant results merely because we have removed too many samples.

y <- c(2011, 2013, 2001, 2006, 2023)
m1c <- update(m1, data = filter(v, !year %in% y))
m2c <- update(m2, data = filter(v, !year %in% y))
models_c <- list(m1c, m2c)

Comparing the summary tables shows only superficial differences.

Data saved to Data/Datasets/table_supplemental.csv

Original

fmt_summary(models, intercept = FALSE)
model Parameter Estimate Std. Error T P
mig_dur_days ~ year year −0.087 0.096 −0.909 0.373
peak_dur_days ~ year year −0.022 0.037 −0.588 0.563

Years removed

fmt_summary(models_c, intercept = FALSE)
tc <- get_table(models_c) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "all_removed")
write_csv(tc, d, append = TRUE)
model Parameter Estimate Std. Error T P
mig_dur_days ~ year year −0.123 0.119 −1.037 0.314
peak_dur_days ~ year year −0.034 0.044 −0.761 0.457

Conclusions

I do not believe that these potentially problematic sampling years are driving the patterns we see in this data.

Code 
map(models, summary)
[[1]]

Call:
lm(formula = mig_dur_days ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.4810 -1.8159  0.6308  2.3101  6.0434 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) 200.07286  193.42774   1.034    0.312
year         -0.08740    0.09618  -0.909    0.373

Residual standard error: 3.445 on 22 degrees of freedom
Multiple R-squared:  0.03618,   Adjusted R-squared:  -0.007629 
F-statistic: 0.8259 on 1 and 22 DF,  p-value: 0.3733


[[2]]

Call:
lm(formula = peak_dur_days ~ year, data = v)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.5892 -0.5837  0.2901  1.2242  1.6083 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 53.68286   75.07369   0.715    0.482
year        -0.02195    0.03733  -0.588    0.563

Residual standard error: 1.337 on 22 degrees of freedom
Multiple R-squared:  0.01547,   Adjusted R-squared:  -0.02928 
F-statistic: 0.3457 on 1 and 22 DF,  p-value: 0.5625

Number of birds in kettles

What is the maximum kettle count? Has this changed?

  • Look for changes in the maximum predicted count and in the maximum observed count
  • variables mig_pop_max, mig_raw_max
  • In both cases, these values represent the maximum population counts for the migration period (25%-75%), but also correspond the the maximum population count overall.

Descriptive stats

Code 
v |> 
  select("mig_pop_max", "mig_raw_max") |>
  desc_stats()
measure mean sd min median max n
mig_pop_max 442.38 236.76 141 351 1304 24
mig_raw_max 831.00 471.99 310 665 2375 24

Here we use a Negative Binomial Generalized Linear Model.

  • The linear regression was a bit iffy (especially for the raw counts which are more volatile), although a log transformation helped.
  • However, since the data is technically count data (i.e. kettle counts, predicted and raw), theoretically is it Poisson distributed data.
  • So I tried Poisson models, but they were overdispersed
  • Therefore, I use a Negative Binomial distribution to model the dispersion directly
  • This ends up with very similar results to log-transformed linear regression, but is a more appropriate given the type of data.

However we can easily present log10 models if you think that’s simpler to present.

  • I also ran a third NB model (m2b), which omitted some of the really large raw kettle counts (see the Figure), because these really large counts resulted in some problems in the model residual figure (see Model Checks)
  • Removing the counts resulted in better model fit, and didn’t really change the interpretations (see the results under mig_raw_max where the sample size is only 23.
  • Therefore, I think I wouldn’t worry about the model checks and would keep model m2 (the results saved to file only include the first two models).
m1 <- MASS::glm.nb(mig_pop_max ~ year, data = v)
m2 <- MASS::glm.nb(mig_raw_max ~ year, data = v)
m2b <- MASS::glm.nb(mig_raw_max ~ year, data = filter(v, mig_raw_max < 1500))

models <- list(m1, m2, m2b)

Not used, but included for completeness

x1 <- lm(log10(mig_pop_max) ~ year, data = v)
x2 <- lm(log10(mig_raw_max) ~ year, data = v)

y1 <- glm(mig_pop_max ~ year, family = "poisson", data = v)
y2 <- glm(mig_raw_max ~ year, family = "poisson", data = v)

s <- simulateResiduals(x1, plot = TRUE)
title("log10 - mig_pop_max ~ year")

s <- simulateResiduals(x2, plot = TRUE)
title("log10 - mig_raw_max ~ year")

s <- simulateResiduals(y1, plot = TRUE)
title("Poisson - mig_pop_max ~ year")

s <- simulateResiduals(y2, plot = TRUE)
title("Poisson - mig_raw_max ~ year")

Tabulated Results

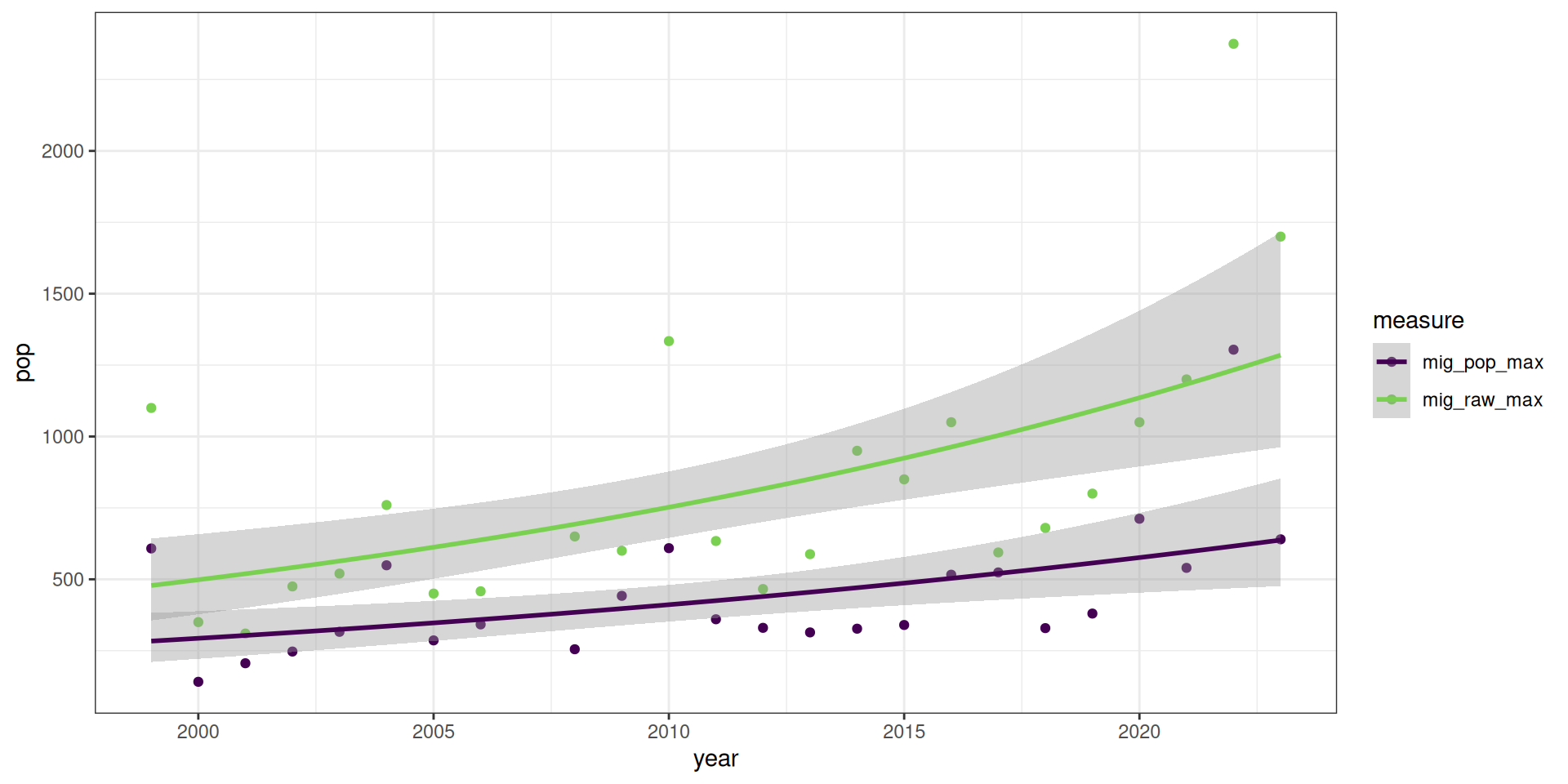
All the measures are significant. There was an increase in the maximum number of birds in kettles in both the raw counts as well as the predicted max.

Code 
t <- get_table(models)
write_csv(filter(t, n != 23), "Data/Datasets/table_pop_mig.csv")
fmt_table(t)
term estimate estimate exp std error statistic p value n
mig_pop_max ~ year
(Intercept) −61.797 0.000 21.547 −2.868 0.004 24
year 0.034 1.034 0.011 3.149 0.002 24
mig_raw_max ~ year
(Intercept) −76.141 0.000 21.342 −3.568 0.000 24
year 0.041 1.042 0.011 3.880 0.000 24
(Intercept) −45.812 0.000 21.627 −2.118 0.034 22
year 0.026 1.026 0.011 2.422 0.015 22
Code 
pop_figs <- v |>
  select(year, mig_pop_max, mig_raw_max) |>
  pivot_longer(-year, names_to = "measure", values_to = "pop")

ggplot(pop_figs, aes(x = year, y = pop, group = measure, colour = measure)) +
  theme_bw() +
  geom_point() +
  stat_smooth(method = MASS::glm.nb) +
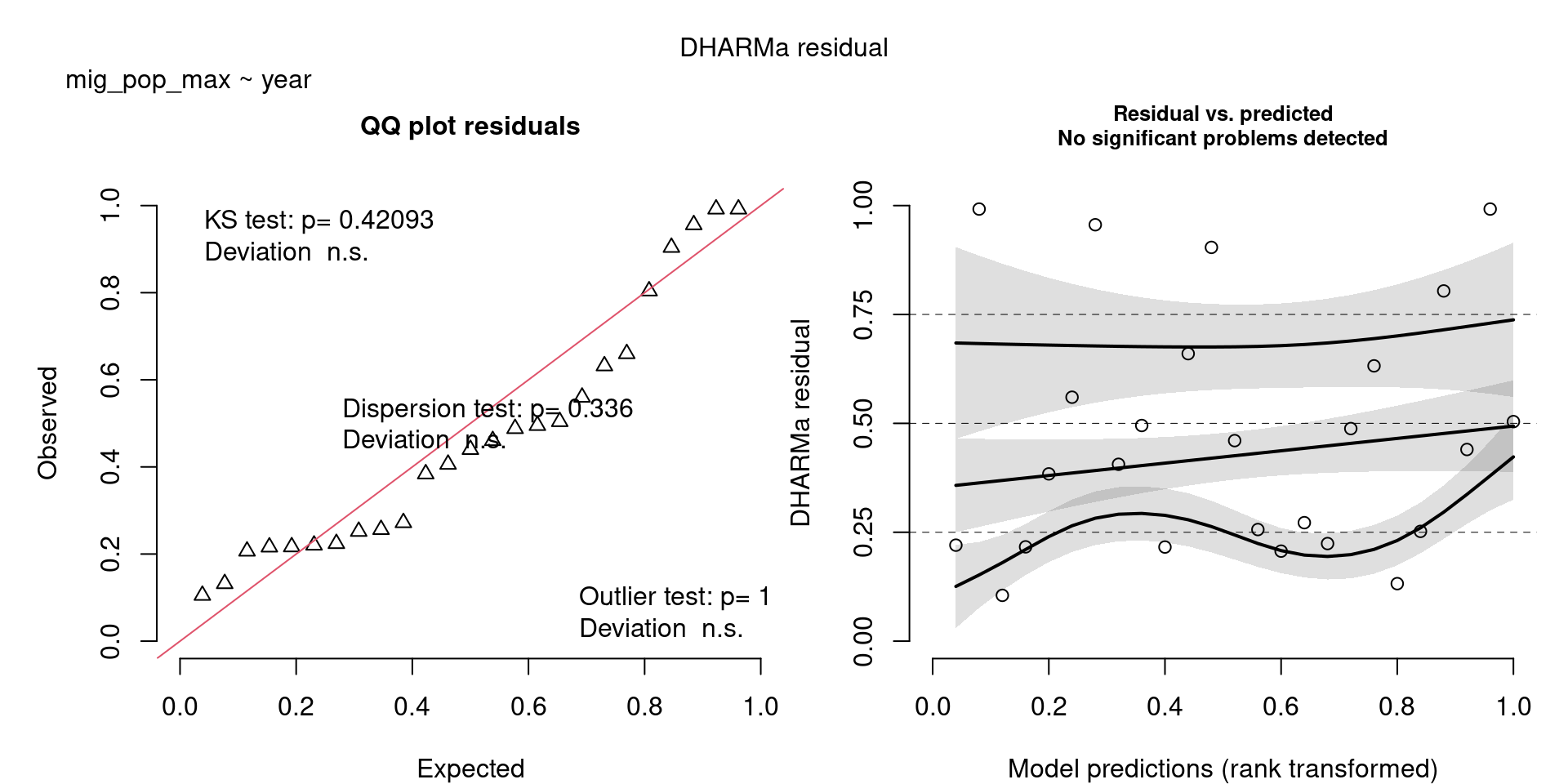
  scale_colour_viridis_d(end = 0.8)
`geom_smooth()` using formula = 'y ~ x'

Code 
model_check_figs(models)

The DHARMa model checks don’t highlight any particular outlier problems, but out of an abundance of caution, we’ll do a quick review of any high Cook’s D values.

Values highlighted in red are less than 4/25, a standard Cook’s D cutoff (4/sample size). These indicate potential influential data points for a particular model.

Code 
get_cooks(models[-3]) |>
  gt_cooks()
Cook's Distances
year mig_pop_max mig_raw_max
1999 0.97 1.28
2000 0.17 0.06
2001 0.06 0.09
2002 0.02 0.01
2003 0.00 0.00
2004 0.13 0.03
2005 0.01 0.02
2006 0.00 0.02
2008 0.02 0.00
2009 0.00 0.00
2010 0.04 0.10
2011 0.00 0.01
2012 0.01 0.03
2013 0.02 0.02
2014 0.02 0.00
2015 0.02 0.00
2016 0.00 0.00
2017 0.00 0.05
2018 0.05 0.04
2019 0.04 0.03
2020 0.02 0.00
2021 0.00 0.00
2022 0.76 0.53
2023 0.00 0.08

Check influential points

Now let’s see what happens if we were to omit these years from the respective analyses.

Tables with coefficients for both original and new model are shown, with colour intensity showing strength in the pattern.

For the maximum population recorded during migration based on both predicted counts and raw counts, if we omit 1999, the patterns are stronger, but the same.

compare(m1, 1999)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - mig_pop_max (Intercept) -61.797 21.547 -2.868 0.004
Drop 1999 - mig_pop_max (Intercept) -88.105 19.999 -4.405 0.000
Original - mig_pop_max year 0.034 0.011 3.149 0.002
Drop 1999 - mig_pop_max year 0.047 0.010 4.707 0.000 
compare(m2, 1999)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - mig_raw_max (Intercept) -76.141 21.342 -3.568 0
Drop 1999 - mig_raw_max (Intercept) -106.053 18.756 -5.654 0
Original - mig_raw_max year 0.041 0.011 3.880 0
Drop 1999 - mig_raw_max year 0.056 0.009 6.008 0

If we omit 2000 or 2022, the patterns are weaker, but still the same.

compare(m1, 2000)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - mig_pop_max (Intercept) -61.797 21.547 -2.868 0.004
Drop 2000 - mig_pop_max (Intercept) -53.042 21.731 -2.441 0.015
Original - mig_pop_max year 0.034 0.011 3.149 0.002
Drop 2000 - mig_pop_max year 0.029 0.011 2.721 0.006 
compare(m1, 2022)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - mig_pop_max (Intercept) -61.797 21.547 -2.868 0.004
Drop 2022 - mig_pop_max (Intercept) -40.321 19.944 -2.022 0.043
Original - mig_pop_max year 0.034 0.011 3.149 0.002
Drop 2022 - mig_pop_max year 0.023 0.010 2.322 0.020 
compare(m2, 2022)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - mig_raw_max (Intercept) -76.141 21.342 -3.568 0.000
Drop 2022 - mig_raw_max (Intercept) -59.119 20.655 -2.862 0.004
Original - mig_raw_max year 0.041 0.011 3.880 0.000
Drop 2022 - mig_raw_max year 0.033 0.010 3.182 0.001

Therefore I wouldn’t be concerned

In addition to the sensitivity check using cook’s distances, here we will conduct a more targeted exploration of some specific years.

Gaps around the peak

First, we consider removing 2011 and 2013 as they have sampling gaps around the peak of migration

y <- c(2011, 2013)
m1a <- update(m1, data = filter(v, !year %in% y))
m2a <- update(m2, data = filter(v, !year %in% y))
models_a <- list(m1a, m2a)

Comparing the summary tables shows only superficial differences.

Data saved to Data/Datasets/table_supplemental.csv

Original

fmt_summary(models[1:2], intercept = FALSE)
to <- get_table(models[1:2]) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "original")
write_csv(to, d, append = TRUE)
model Parameter Estimate Std. Error Z P
mig_pop_max ~ year year 0.034 0.011 3.149 0.002
mig_raw_max ~ year year 0.041 0.011 3.880 0.000

Years removed

fmt_summary(models_a, intercept = FALSE)
ta <- get_table(models_a) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "gaps_removed")
write_csv(ta, d, append = TRUE)
model Parameter Estimate Std. Error Z P
mig_pop_max ~ year year 0.034 0.011 3.117 0.002
mig_raw_max ~ year year 0.042 0.011 3.842 0.000

Missing the end of migration

Second, we consider removing 2001, 2006, 2023 as they were three years where it looks like sampling ended earlier than the end of migration.

y <- c(2001, 2006, 2023)
m1b <- update(m1, data = filter(v, !year %in% y))
m2b <- update(m2, data = filter(v, !year %in% y))
models_b <- list(m1b, m2b)

Comparing the summary tables shows only superficial differences.

Data saved to Data/Datasets/table_supplemental.csv

Original

fmt_summary(models[1:2], intercept = FALSE)
model Parameter Estimate Std. Error Z P
mig_pop_max ~ year year 0.034 0.011 3.149 0.002
mig_raw_max ~ year year 0.041 0.011 3.880 0.000

Years removed

fmt_summary(models_b, intercept = FALSE)
tb <- get_table(models_b) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "end_removed")
write_csv(tb, d, append = TRUE)
model Parameter Estimate Std. Error Z P
mig_pop_max ~ year year 0.031 0.013 2.439 0.015
mig_raw_max ~ year year 0.033 0.012 2.811 0.005

Remove all problematic years

Out of curiosity, let’s try removing all 5 years. This reduces our data from 25 to 19 samples, so is a substantial change and we may see non-significant results merely because we have removed too many samples.

y <- c(2011, 2013, 2001, 2006, 2023)
m1c <- update(m1, data = filter(v, !year %in% y))
m2c <- update(m2, data = filter(v, !year %in% y))
models_c <- list(m1c, m2c)

Comparing the summary tables shows only superficial differences.

Data saved to Data/Datasets/table_supplemental.csv

Original

fmt_summary(models[1:2], intercept = FALSE)
model Parameter Estimate Std. Error Z P
mig_pop_max ~ year year 0.034 0.011 3.149 0.002
mig_raw_max ~ year year 0.041 0.011 3.880 0.000

Years removed

fmt_summary(models_c, intercept = FALSE)
tc <- get_table(models_c) |>
  select(model, term, estimate, std_error, statistic, p_value) |>
  mutate(type = "all_removed")
write_csv(tc, d, append = TRUE)
model Parameter Estimate Std. Error Z P
mig_pop_max ~ year year 0.031 0.013 2.411 0.016
mig_raw_max ~ year year 0.034 0.012 2.790 0.005

Conclusions

I do not believe that these potentially problematic sampling years are driving the patterns we see in this data.

Code 
map(models, summary)
[[1]]

Call:
MASS::glm.nb(formula = mig_pop_max ~ year, data = v, init.theta = 6.906339287, 
    link = log)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)   
(Intercept) -61.79691   21.54677  -2.868  0.00413 **
year          0.03374    0.01071   3.149  0.00164 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(6.9063) family taken to be 1)

    Null deviance: 35.662  on 23  degrees of freedom
Residual deviance: 24.554  on 22  degrees of freedom
AIC: 316.49

Number of Fisher Scoring iterations: 1

              Theta:  6.91 
          Std. Err.:  1.98 

 2 x log-likelihood:  -310.494 

[[2]]

Call:
MASS::glm.nb(formula = mig_raw_max ~ year, data = v, init.theta = 6.987056274, 
    link = log)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -76.14124   21.34238  -3.568 0.000360 ***
year          0.04118    0.01061   3.880 0.000104 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(6.9871) family taken to be 1)

    Null deviance: 41.646  on 23  degrees of freedom
Residual deviance: 24.554  on 22  degrees of freedom
AIC: 345.5

Number of Fisher Scoring iterations: 1

              Theta:  6.99 
          Std. Err.:  1.99 

 2 x log-likelihood:  -339.505 

[[3]]

Call:
MASS::glm.nb(formula = mig_raw_max ~ year, data = filter(v, mig_raw_max < 
    1500), init.theta = 8.726319225, link = log)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)  
(Intercept) -45.81205   21.62744  -2.118   0.0342 *
year          0.02606    0.01076   2.422   0.0154 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(8.7263) family taken to be 1)

    Null deviance: 28.568  on 21  degrees of freedom
Residual deviance: 22.414  on 20  degrees of freedom
AIC: 308.17

Number of Fisher Scoring iterations: 1

              Theta:  8.73 
          Std. Err.:  2.62 

 2 x log-likelihood:  -302.166

Number of residents

How many resident vultures are there? Has this changed?

  • Look for changes in the median number of residents
  • res_pop_median, res_raw_median

Descriptive stats

Code 
v |> 
  select("res_pop_median", "res_raw_median") |>
  desc_stats()
measure mean sd min median max n
res_pop_median 5.62 2.68 2 5.0 12 24
res_raw_median 4.96 2.14 1 4.5 8 24

Here we use a Poisson Generalized Linear Model.

  • This yields similar results to a linear regression with log transformed values.
  • However, since the data is technically count data (i.e. kettle counts, predicted and raw), theoretically is it Poisson distributed data.
  • It is not overdispersed so we stick with Poisson (rather than Negative Binomial as we did above)
m1 <- glm(res_pop_median ~ year, family = "poisson", data = v)
m2 <- glm(res_raw_median ~ year, family = "poisson", data = v)

models <- list(m1, m2)

Not used, but included for completeness

x1 <- lm(log10(res_pop_median) ~ year, data = v)
x2 <- lm(log10(res_raw_median) ~ year, data = v)

s <- simulateResiduals(x1, plot = TRUE)
Warning in newton(lsp = lsp, X = G$X, y = G$y, Eb = G$Eb, UrS = G$UrS, L = G$L,
: Fitting terminated with step failure - check results carefully
title("log10 - res_pop_median ~ year")

s <- simulateResiduals(x2, plot = TRUE)
title("log10 - res_raw_median ~ year")

Tabulated Results

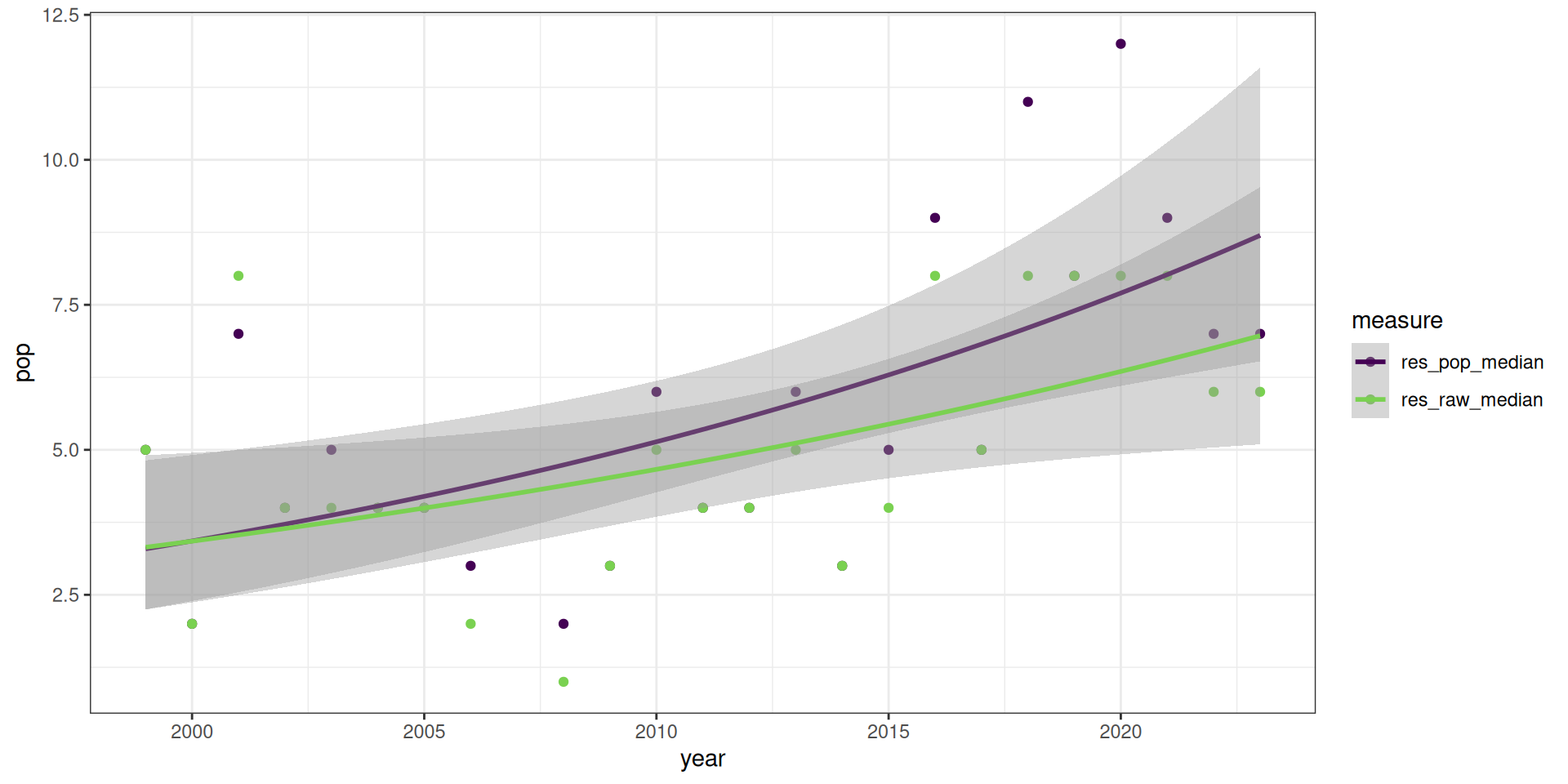
All measures are significant, there is an increase in the number of resident birds over the years.

Code 
t <- get_table(models)
write_csv(t, "Data/Datasets/table_pop_res.csv")
fmt_table(t)
term estimate estimate exp std error statistic p value n
res_pop_median ~ year
(Intercept) −79.712 0.000 24.549 −3.247 0.001 24
year 0.040 1.041 0.012 3.319 0.001 24
res_raw_median ~ year
(Intercept) −60.538 0.000 25.804 −2.346 0.019 24
year 0.031 1.031 0.013 2.409 0.016 24
Code 
res_figs <- v |>
  select(year, res_pop_median, res_raw_median) |>
  pivot_longer(-year, names_to = "measure", values_to = "pop")

ggplot(res_figs, aes(x = year, y = pop, group = measure, colour = measure)) +
  theme_bw() +
  geom_point() +
  geom_smooth(method = "glm", method.args = list(family = "poisson")) +
  scale_colour_viridis_d(end = 0.8)
`geom_smooth()` using formula = 'y ~ x'

Code 
model_check_figs(models)

The DHARMa model checks don’t highlight any particular outlier problems, but out of an abundance of caution, we’ll do a quick review of any high Cook’s D values.

Values highlighted in red are less than 4/25, a standard Cook’s D cutoff (4/sample size). These indicate potential influential data points for a particular model.

Code 
get_cooks(models) |>
  gt_cooks()
Cook's Distances
year res_pop_median res_raw_median
1999 0.07 0.07
2000 0.04 0.05
2001 0.22 0.39
2002 0.00 0.00
2003 0.02 0.00
2004 0.00 0.00
2005 0.00 0.00
2006 0.02 0.04
2008 0.05 0.08
2009 0.02 0.01
2010 0.00 0.00
2011 0.01 0.00
2012 0.01 0.00
2013 0.00 0.00
2014 0.04 0.02
2015 0.01 0.01
2016 0.03 0.03
2017 0.02 0.00
2018 0.10 0.03
2019 0.00 0.03
2020 0.16 0.03
2021 0.01 0.03
2022 0.02 0.01
2023 0.05 0.02

Check influential points

Now let’s see what happens if we were to omit these years from the respective analyses.

Tables with coefficients for both original and new model are shown, with colour intensity showing strength in the pattern.

For the daily median number of resident birds based on both predicted counts and raw counts, if we omit 2001, the patterns are stronger, but the same.

compare(m1, 2001)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - res_pop_median (Intercept) -79.712 24.549 -3.247 0.001
Drop 2001 - res_pop_median (Intercept) -94.397 26.293 -3.590 0.000
Original - res_pop_median year 0.040 0.012 3.319 0.001
Drop 2001 - res_pop_median year 0.048 0.013 3.658 0.000 
compare(m2, 2001)
model parameter Estimate Std. Error z value Pr(>|z|)
Original - res_raw_median (Intercept) -60.538 25.804 -2.346 0.019
Drop 2001 - res_raw_median (Intercept) -81.261 27.918 -2.911 0.004
Original - res_raw_median year 0.031 0.013 2.409 0.016
Drop 2001 - res_raw_median year 0.041 0.014 2.969 0.003

Therefore I wouldn’t be concerned

Code 
map(models, summary)
[[1]]

Call:
glm(formula = res_pop_median ~ year, family = "poisson", data = v)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -79.71246   24.54876  -3.247 0.001166 ** 
year          0.04047    0.01219   3.319 0.000903 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 28.293  on 23  degrees of freedom
Residual deviance: 16.914  on 22  degrees of freedom
AIC: 104.74

Number of Fisher Scoring iterations: 4


[[2]]

Call:
glm(formula = res_raw_median ~ year, family = "poisson", data = v)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)  
(Intercept) -60.53757   25.80385  -2.346    0.019 *
year          0.03088    0.01282   2.409    0.016 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 22.313  on 23  degrees of freedom
Residual deviance: 16.391  on 22  degrees of freedom
AIC: 101.33

Number of Fisher Scoring iterations: 4

Patterns of migration

Is the timing of migration skewed to earlier or later in the season? Is this distribution of migration flattened and wide (low kurtosis) or peaked (high kurtosis) Are these patterns consistent over the years?

Kurtosis can be used to indicates if all the birds pass through in a relatively quick ‘clump’ (thick-tailed, lower kurtosis), or whether the migration stretches out over a longer period of time (long-tailed, higher kurtosis). Possible implications for conservation or future survey designs?

  • Look for significant skew and kurtosis in migration (5-95%) and peak migration (25-75%)
  • mig_skew, peak_skew, mig_kurt, peak_kurt

Descriptive stats

Code 
v |> 
  select(contains("skew"), contains("kurt")) |>
  desc_stats()
measure mean sd min median max n
mig_skew 0.00 0.21 -0.4442868 -0.03392198 0.5067799 24
peak_skew 0.00 0.09 -0.1296424 -0.02295204 0.2880288 24
all_skew −0.06 0.20 -0.4654119 -0.05317408 0.3816406 24
mig_kurt −0.67 0.17 -0.9329652 -0.71138435 -0.1280714 24
peak_kurt −1.12 0.03 -1.1883554 -1.12398983 -1.0337500 24
all_kurt 0.27 0.58 -0.3319748 0.20767601 2.5554292 24

Here we look at skew and excess kurtosis only against the intercept. This allows us to test for differences from 0.

  • Skew of 0 is normal, but below or above are considered left- and right-skewed
  • A normal distribution has an excess kurtosis of 0.

So here, we are not asking if skew or kurtosis changes over the years, just whether it is different from normal (0).

m1 <- lm(mig_skew ~ 1, data = v)
m2 <- lm(peak_skew ~ 1, data = v)
m3 <- lm(all_skew ~ 1, data = v)
m4 <- lm(mig_kurt ~ 1, data = v)
m5 <- lm(peak_kurt ~ 1, data = v)
m6 <- lm(all_kurt ~ 1, data = v)

models <- list(m1, m2, m3, m4, m5, m6)

Tabulated Results

Skew is not significantly different from zero in any period.

Kurtosis is significantly different from zero in all periods.

In the migration and peak migration periods, Kurtosis is negative, corresponding to thick-tailed distributions, squat distributions (closer to a uniform distribution).

However, in the ‘all’ period, kurtosis is actually significantly positive, corresponding to relatively more narrow, thin-tailed distributions.

Code 
t <- get_table(models)
write_csv(t, "Data/Datasets/table_skew.csv")
fmt_table(t)
term estimate std error statistic p value n
mig_skew ~ 1 (R2 = 0; R2-adj = 0)
(Intercept) −0.003 0.042 −0.067 0.947 24
peak_skew ~ 1 (R2 = 0; R2-adj = 0)
(Intercept) −0.003 0.018 −0.166 0.869 24
all_skew ~ 1 (R2 = 0; R2-adj = 0)
(Intercept) −0.063 0.041 −1.531 0.139 24
mig_kurt ~ 1 (R2 = 0; R2-adj = 0)
(Intercept) −0.674 0.034 −19.567 0.000 24
peak_kurt ~ 1 (R2 = 0; R2-adj = 0)
(Intercept) −1.124 0.006 −174.493 0.000 24
all_kurt ~ 1 (R2 = 0; R2-adj = 0)
(Intercept) 0.267 0.119 2.246 0.035 24

The periods

The “all” period is defined individually as being the dates centred on the date at the 50% percentile passage is reached and includes all dates from this date to the end of the year, and that same number of dates prior to the p50 date. See the Skewness & Kurtosis section in the last report.

By definition, the migration period (5-95%) and the peak migration period (25-75%) are truncated distributions, so I don’t think we can really interpret kurtosis for these subsets. With the “all” period, I have attempted to subset the data to get a good measure of the migration period only, but honestly, kurtosis depends so much on where I define the cutoffs I’m not really sure that we can accurately measure it. Looking at the figures, I’d say they’re narrower than normal (so positive kurtosis, which does align with the stats for the “all” period), but that’s just a visual estimate.

This is figure showing the statistics.

Code 
dist_figs <- v |>
  select(year, contains("skew"), contains("kurt")) |>
  pivot_longer(cols = -year, names_to = "measure", values_to = "statistic")

ggplot(filter(dist_figs, year != 2001), aes(x = statistic, y = measure, fill = measure)) +
  theme_bw() +
  geom_vline(xintercept = 0, colour = "grey20", linetype = "dotted") +
  geom_boxplot() +
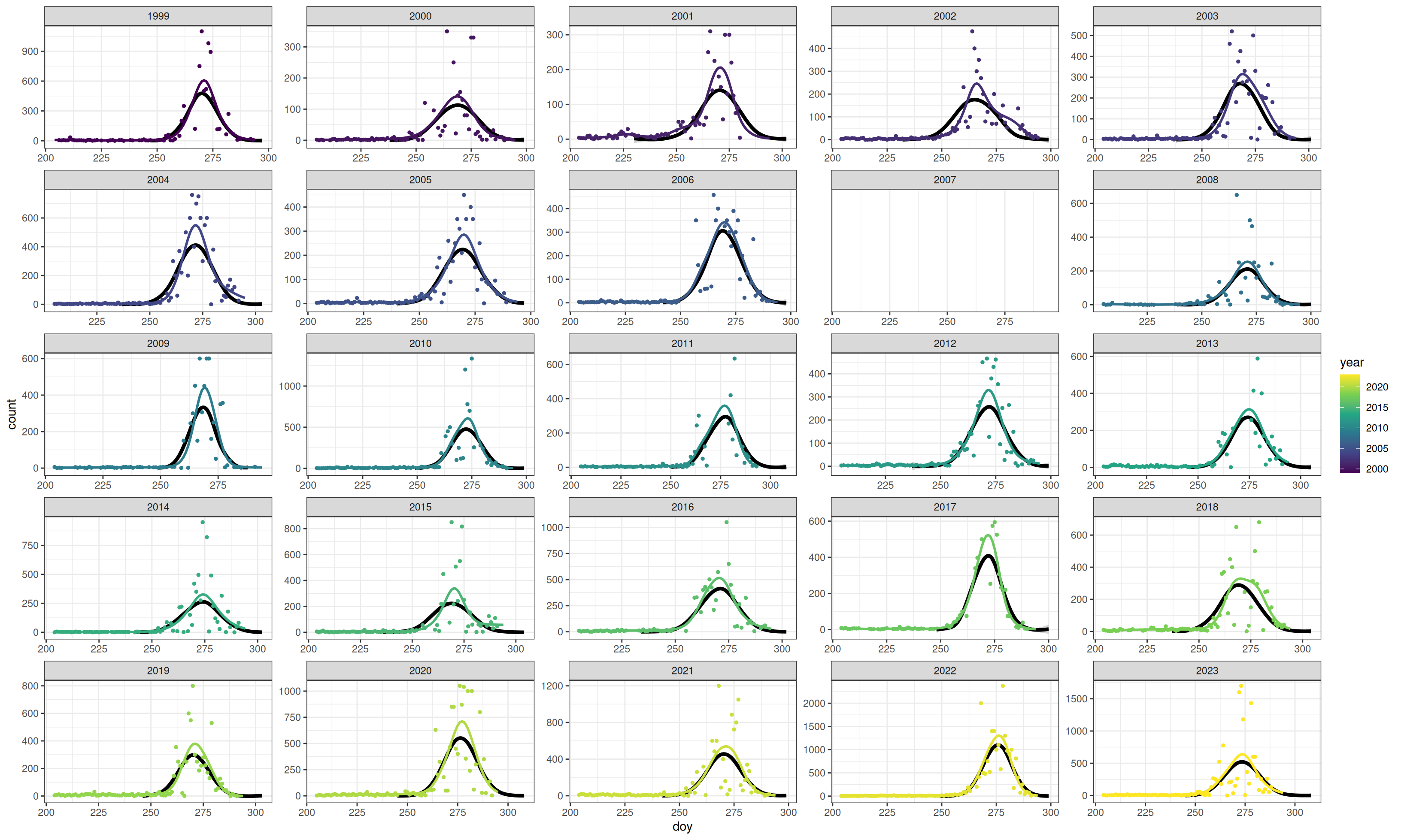
  scale_fill_viridis_d()

This figure shows the distributions in each year over top a normal distribution, for illustration.

I think this shows positive kurtosis. The black lines are simulated normal distributions simulated using the mean, SD and counts from the data.

Code 
normal <- v |>
  select(year, max_doy, mig_pop_total) |>
  left_join(summarize(filter(pred, doy > 240), sd = sd(rep(doy, round(count))), .by = "year"), 
            by = "year") |>
  mutate(doy = pmap(list(max_doy, sd, mig_pop_total),
                    \(x, y, z) as.integer(rnorm(mean = x, sd = y, n = z)))) |>
  unnest(doy) |>
  count(year, doy, name = "count")

ggplot(raw, aes(x = doy, y = count)) + 
  theme_bw() +
  geom_smooth(data = normal, method = "gam", colour = "black", linewidth = 1.5) +
  geom_point(size = 1, aes(colour = year), na.rm = TRUE) + 
  geom_line(data = pred, linewidth = 1, aes(group = year, colour = year), na.rm = TRUE) +
  scale_colour_viridis_c() +
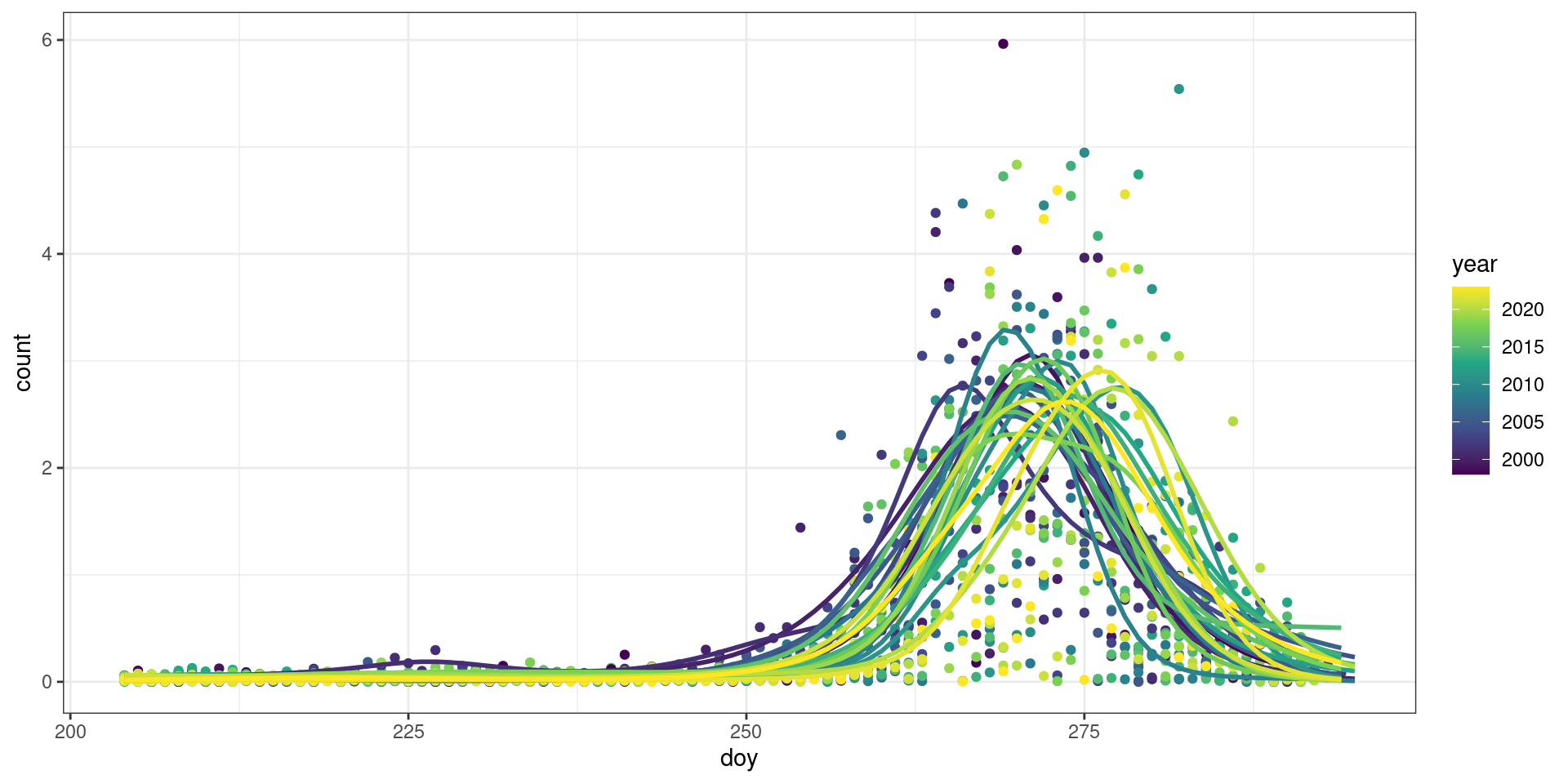
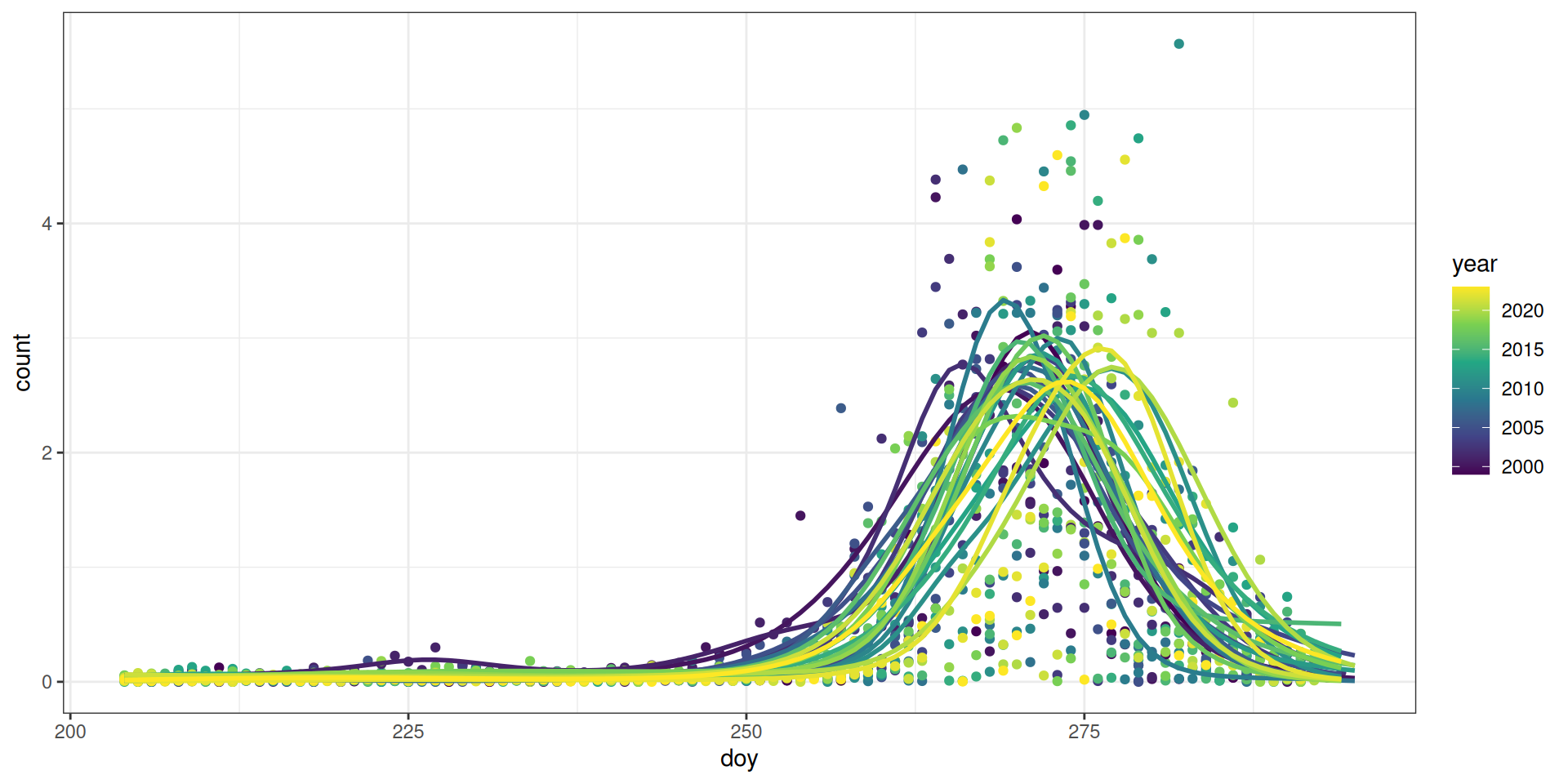
  facet_wrap(~year, scales = "free")
`geom_smooth()` using formula = 'y ~ s(x, bs = "cs")'

Here is a scaled view (counts are divided by the yearly standard deviation) of the patterns of migration using our GAM models from the “Calculate Metrics” step.

Code 
raw_scaled <- raw |>
  mutate(across(c(count), \(x) scale(x, center = FALSE)),
         .by = "year")

pred_scaled <- pred |>
  mutate(across(c(count, ci99_upper, ci99_lower), \(x) scale(x, center = FALSE)),
         .by = "year")
           
ggplot(raw_scaled, aes(x = doy, y = count)) + 
  theme_bw() +
  geom_point(aes(colour = year), na.rm = TRUE) +
  geom_line(data = pred_scaled, aes(colour = year, group = year), 
            size = 1, na.rm = TRUE) +
  scale_colour_viridis_c()
Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

Code 
model_check_figs(models)

The DHARMa model checks don’t highlight any particular outlier problems, but out of an abundance of caution, we’ll do a quick review of any high Cook’s D values.

Values highlighted in red are less than 4/25, a standard Cook’s D cutoff (4/sample size). These indicate potential influential data points for a particular model.

Code 
get_cooks(models) |>
  gt_cooks()
Cook's Distances
year mig_skew ~ 1 peak_skew ~ 1 all_skew ~ 1 mig_kurt ~ 1 peak_kurt ~ 1 all_kurt ~ 1
1999 0.01 0.00 0.01 0.00 0.00 0.04
2000 0.02 0.03 0.02 0.00 0.00 0.00
2001 0.21 0.05 0.18 0.17 0.00 0.00
2002 0.16 0.47 0.05 0.00 0.37 0.01
2003 0.02 0.05 0.02 0.03 0.03 0.01
2004 0.15 0.09 0.21 0.09 0.08 0.00
2005 0.00 0.00 0.00 0.00 0.01 0.00
2006 0.00 0.00 0.00 0.03 0.00 0.02
2008 0.05 0.02 0.09 0.00 0.00 0.00
2009 0.00 0.00 0.02 0.00 0.08 0.70
2010 0.00 0.04 0.01 0.01 0.01 0.01
2011 0.04 0.09 0.01 0.02 0.00 0.05
2012 0.00 0.00 0.01 0.01 0.00 0.00
2013 0.00 0.00 0.00 0.02 0.00 0.04
2014 0.00 0.00 0.00 0.00 0.03 0.03
2015 0.28 0.10 0.22 0.47 0.13 0.00
2016 0.02 0.00 0.03 0.00 0.00 0.00
2017 0.03 0.03 0.05 0.00 0.00 0.03
2018 0.00 0.01 0.01 0.11 0.19 0.04
2019 0.01 0.01 0.04 0.03 0.01 0.01
2020 0.01 0.01 0.00 0.00 0.01 0.03
2021 0.02 0.01 0.02 0.02 0.07 0.00
2022 0.01 0.03 0.02 0.01 0.04 0.00
2023 0.00 0.01 0.00 0.00 0.00 0.02

Check influential points

Now let’s see what happens if we were to omit these years from the respective analyses.

Tables with coefficients for both original and new model are shown, with colour intensity showing strength in the pattern.

For 2001, the patterns shift but do not change.

compare(m1, 2001)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_skew ~ 1 (Intercept) -0.003 0.042 -0.067 0.947
Drop 2001 - mig_skew ~ 1 (Intercept) 0.016 0.039 0.418 0.680 
compare(m3, 2001)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - all_skew ~ 1 (Intercept) -0.063 0.041 -1.531 0.139
Drop 2001 - all_skew ~ 1 (Intercept) -0.045 0.039 -1.169 0.255 
compare(m4, 2001)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_kurt ~ 1 (Intercept) -0.674 0.034 -19.567 0
Drop 2001 - mig_kurt ~ 1 (Intercept) -0.688 0.033 -21.016 0

For 2002, the patterns are stronger.

compare(m2, 2002)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_skew ~ 1 (Intercept) -0.003 0.018 -0.166 0.869
Drop 2002 - peak_skew ~ 1 (Intercept) -0.016 0.014 -1.121 0.275 
compare(m5, 2002)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_kurt ~ 1 (Intercept) -1.124 0.006 -174.493 0
Drop 2002 - peak_kurt ~ 1 (Intercept) -1.128 0.005 -211.632 0

For skew of the counts during the “all” period, if we omit 2004, the patterns are stronger, and nearly show a trend, but are still non-significant.

compare(m3, 2004)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - all_skew ~ 1 (Intercept) -0.063 0.041 -1.531 0.139
Drop 2004 - all_skew ~ 1 (Intercept) -0.082 0.038 -2.147 0.043

For kurtosis during the “all” migration period, if we omit 2009, the patterns are less strong, but the same.

compare(m6, 2009)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - all_kurt ~ 1 (Intercept) 0.267 0.119 2.246 0.035
Drop 2009 - all_kurt ~ 1 (Intercept) 0.167 0.068 2.467 0.022

For 2015, the patterns are stronger, but the same (i.e., not significant).

compare(m1, 2015)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_skew ~ 1 (Intercept) -0.003 0.042 -0.067 0.947
Drop 2015 - mig_skew ~ 1 (Intercept) -0.025 0.037 -0.667 0.512 
compare(m3, 2015)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - all_skew ~ 1 (Intercept) -0.063 0.041 -1.531 0.139
Drop 2015 - all_skew ~ 1 (Intercept) -0.082 0.038 -2.172 0.041 
compare(m4, 2015)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - mig_kurt ~ 1 (Intercept) -0.674 0.034 -19.567 0
Drop 2015 - mig_kurt ~ 1 (Intercept) -0.697 0.026 -26.758 0

For kurtosis during the peak migration period, if we omit 2018, the patterns don’t really change.

compare(m5, 2018)
model parameter Estimate Std. Error t value Pr(>|t|)
Original - peak_kurt ~ 1 (Intercept) -1.124 0.006 -174.493 0
Drop 2018 - peak_kurt ~ 1 (Intercept) -1.121 0.006 -184.887 0

Therefore I wouldn’t be concerned

Code 
map(models, summary)
[[1]]

Call:
lm(formula = mig_skew ~ 1, data = v)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.44147 -0.11385 -0.03111  0.07105  0.50959 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.002813   0.042126  -0.067    0.947

Residual standard error: 0.2064 on 23 degrees of freedom


[[2]]

Call:
lm(formula = peak_skew ~ 1, data = v)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.12657 -0.06225 -0.01988  0.02682  0.29110 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.003073   0.018460  -0.166    0.869

Residual standard error: 0.09044 on 23 degrees of freedom


[[3]]

Call:
lm(formula = all_skew ~ 1, data = v)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.40252 -0.13270  0.00971  0.08692  0.44453 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.06289    0.04108  -1.531    0.139

Residual standard error: 0.2012 on 23 degrees of freedom


[[4]]

Call:
lm(formula = mig_kurt ~ 1, data = v)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.25928 -0.10693 -0.03770  0.04197  0.54561 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.67368    0.03443  -19.57 7.79e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1687 on 23 degrees of freedom


[[5]]

Call:
lm(formula = peak_kurt ~ 1, data = v)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.064172 -0.013194  0.000194  0.006965  0.090433 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.124183   0.006443  -174.5   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.03156 on 23 degrees of freedom


[[6]]

Call:
lm(formula = all_kurt ~ 1, data = v)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.59881 -0.36626 -0.05916  0.15063  2.28859 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   0.2668     0.1188   2.246   0.0346 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5821 on 23 degrees of freedom

Reproducibility

Code 
devtools::session_info()
─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.5.1 (2025-06-13)
 os       Ubuntu 24.04.2 LTS
 system   x86_64, linux-gnu
 ui       X11
 language en_CA:en_US:en
 collate  en_CA.UTF-8
 ctype    en_CA.UTF-8
 tz       America/Winnipeg
 date     2025-09-05
 pandoc   3.4 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/x86_64/ (via rmarkdown)
 quarto   1.6.39 @ /usr/local/bin/quarto

─ Packages ───────────────────────────────────────────────────────────────────
 ! package       * version date (UTC) lib source
 P abind           1.4-8   2024-09-12 [?] CRAN (R 4.5.0)
 P assertr       * 3.0.1   2023-11-23 [?] CRAN (R 4.5.0)
 P backports       1.5.0   2024-05-23 [?] CRAN (R 4.5.0)
 P bit             4.6.0   2025-03-06 [?] CRAN (R 4.5.0)
 P bit64           4.6.0-1 2025-01-16 [?] CRAN (R 4.5.0)
 P boot            1.3-31  2024-08-28 [?] CRAN (R 4.4.2)
 P broom         * 1.0.8   2025-03-28 [?] CRAN (R 4.5.0)
 P cachem          1.1.0   2024-05-16 [?] CRAN (R 4.5.0)
 P car             3.1-3   2024-09-27 [?] CRAN (R 4.5.0)
 P carData         3.0-5   2022-01-06 [?] CRAN (R 4.5.0)
 P cellranger      1.1.0   2016-07-27 [?] CRAN (R 4.5.0)
 P class           7.3-23  2025-01-01 [?] CRAN (R 4.4.2)
 P classInt        0.4-11  2025-01-08 [?] CRAN (R 4.5.0)
 P cli             3.6.5   2025-04-23 [?] CRAN (R 4.5.0)
 P codetools       0.2-20  2024-03-31 [?] CRAN (R 4.4.0)
 P crayon          1.5.3   2024-06-20 [?] CRAN (R 4.5.0)
 P DBI             1.2.3   2024-06-02 [?] CRAN (R 4.5.0)
 P devtools        2.4.5   2022-10-11 [?] CRAN (R 4.5.0)
 P DHARMa        * 0.4.7   2024-10-18 [?] CRAN (R 4.5.0)
 P digest          0.6.37  2024-08-19 [?] CRAN (R 4.5.0)
 P doParallel      1.0.17  2022-02-07 [?] CRAN (R 4.5.0)
 P dplyr         * 1.1.4   2023-11-17 [?] CRAN (R 4.5.0)
 P e1071           1.7-16  2024-09-16 [?] CRAN (R 4.5.0)
 P ellipsis        0.3.2   2021-04-29 [?] CRAN (R 4.5.0)
 P emmeans         1.11.1  2025-05-04 [?] CRAN (R 4.5.0)
 P estimability    1.5.1   2024-05-12 [?] CRAN (R 4.5.0)
 P evaluate        1.0.3   2025-01-10 [?] CRAN (R 4.5.0)
 P farver          2.1.2   2024-05-13 [?] CRAN (R 4.5.0)
 P fastmap         1.2.0   2024-05-15 [?] CRAN (R 4.5.0)
 P foreach         1.5.2   2022-02-02 [?] CRAN (R 4.5.0)
 P Formula         1.2-5   2023-02-24 [?] CRAN (R 4.5.0)
 P fs              1.6.6   2025-04-12 [?] CRAN (R 4.5.0)
 P gamm4           0.2-7   2025-04-22 [?] CRAN (R 4.5.0)
 P gap             1.6     2024-08-27 [?] CRAN (R 4.5.0)
 P gap.datasets    0.0.6   2023-08-25 [?] CRAN (R 4.5.0)
 P generics        0.1.4   2025-05-09 [?] CRAN (R 4.5.0)
 P GGally          2.2.1   2024-02-14 [?] CRAN (R 4.5.0)
 P ggplot2       * 3.5.2   2025-04-09 [?] CRAN (R 4.5.0)
 P ggspatial     * 1.1.9   2023-08-17 [?] CRAN (R 4.5.0)
 P ggstats         0.9.0   2025-03-10 [?] CRAN (R 4.5.0)
 P ggthemes      * 5.1.0   2024-02-10 [?] CRAN (R 4.5.0)
 P glue            1.8.0   2024-09-30 [?] CRAN (R 4.5.0)
 P gridExtra       2.3     2017-09-09 [?] CRAN (R 4.5.0)
 P gt            * 1.0.0   2025-04-05 [?] CRAN (R 4.5.0)
 P gtable          0.3.6   2024-10-25 [?] CRAN (R 4.5.0)
 P hms             1.1.3   2023-03-21 [?] CRAN (R 4.5.0)
 P htmltools       0.5.8.1 2024-04-04 [?] CRAN (R 4.5.0)
 P htmlwidgets     1.6.4   2023-12-06 [?] CRAN (R 4.5.0)
 P httpuv          1.6.16  2025-04-16 [?] CRAN (R 4.5.0)
 P httr            1.4.7   2023-08-15 [?] CRAN (R 4.5.0)
 P iterators       1.0.14  2022-02-05 [?] CRAN (R 4.5.0)
 P jsonlite        2.0.0   2025-03-27 [?] CRAN (R 4.5.0)
 P KernSmooth      2.23-26 2025-01-01 [?] CRAN (R 4.4.2)
 P knitr           1.50    2025-03-16 [?] CRAN (R 4.5.0)
 P labeling        0.4.3   2023-08-29 [?] CRAN (R 4.5.0)
 P later           1.4.2   2025-04-08 [?] CRAN (R 4.5.0)
 P lattice         0.22-7  2025-04-02 [?] CRAN (R 4.5.0)
 P lifecycle       1.0.4   2023-11-07 [?] CRAN (R 4.5.0)
 P lme4            1.1-37  2025-03-26 [?] CRAN (R 4.5.0)
 P lubridate     * 1.9.4   2024-12-08 [?] CRAN (R 4.5.0)
 P magrittr        2.0.3   2022-03-30 [?] CRAN (R 4.5.0)
 P MASS            7.3-65  2025-02-28 [?] CRAN (R 4.4.3)
 P Matrix          1.7-3   2025-03-11 [?] CRAN (R 4.4.3)
 P matrixStats     1.5.0   2025-01-07 [?] CRAN (R 4.5.0)
 P memoise         2.0.1   2021-11-26 [?] CRAN (R 4.5.0)
 P mgcv          * 1.9-3   2025-04-04 [?] CRAN (R 4.5.0)
 P mgcViz        * 0.2.0   2025-04-11 [?] CRAN (R 4.5.0)
 P mime            0.13    2025-03-17 [?] CRAN (R 4.5.0)
 P miniUI          0.1.2   2025-04-17 [?] CRAN (R 4.5.0)
 P minqa           1.2.8   2024-08-17 [?] CRAN (R 4.5.0)
 P moments       * 0.14.1  2022-05-02 [?] CRAN (R 4.5.0)
 P mvtnorm         1.3-3   2025-01-10 [?] CRAN (R 4.5.0)
 P nlme          * 3.1-168 2025-03-31 [?] CRAN (R 4.4.3)
 P nloptr          2.2.1   2025-03-17 [?] CRAN (R 4.5.0)
 P openxlsx      * 4.2.8   2025-01-25 [?] CRAN (R 4.5.0)
 P patchwork     * 1.3.0   2024-09-16 [?] CRAN (R 4.5.0)
 P pillar          1.10.2  2025-04-05 [?] CRAN (R 4.5.0)
 P pkgbuild        1.4.8   2025-05-26 [?] CRAN (R 4.5.0)
 P pkgconfig       2.0.3   2019-09-22 [?] CRAN (R 4.5.0)
 P pkgload         1.4.0   2024-06-28 [?] CRAN (R 4.5.0)
 P plyr            1.8.9   2023-10-02 [?] CRAN (R 4.5.0)
 P profvis         0.4.0   2024-09-20 [?] CRAN (R 4.5.0)
 P promises        1.3.3   2025-05-29 [?] CRAN (R 4.5.0)
 P proxy           0.4-27  2022-06-09 [?] CRAN (R 4.5.0)
 P purrr         * 1.0.4   2025-02-05 [?] CRAN (R 4.5.0)
 P qgam          * 2.0.0   2025-04-10 [?] CRAN (R 4.5.0)
 P R6              2.6.1   2025-02-15 [?] CRAN (R 4.5.0)
 P rbibutils       2.3     2024-10-04 [?] CRAN (R 4.5.0)
 P RColorBrewer    1.1-3   2022-04-03 [?] CRAN (R 4.5.0)
 P Rcpp            1.0.14  2025-01-12 [?] CRAN (R 4.5.0)
 P Rdpack          2.6.4   2025-04-09 [?] CRAN (R 4.5.0)
 P readr         * 2.1.5   2024-01-10 [?] CRAN (R 4.5.0)
 P readxl        * 1.4.5   2025-03-07 [?] CRAN (R 4.5.0)
 P reformulas      0.4.1   2025-04-30 [?] CRAN (R 4.5.0)
 P remotes         2.5.0   2024-03-17 [?] CRAN (R 4.5.0)
 P renv            1.1.4   2025-03-20 [?] CRAN (R 4.5.0)
 P rlang           1.1.6   2025-04-11 [?] CRAN (R 4.5.0)
 P rmarkdown       2.29    2024-11-04 [?] CRAN (R 4.5.0)
 P rnaturalearth * 1.0.1   2023-12-15 [?] CRAN (R 4.5.0)
 P rstudioapi      0.17.1  2024-10-22 [?] CRAN (R 4.5.0)
 P sass            0.4.10  2025-04-11 [?] CRAN (R 4.5.0)
 P scales          1.4.0   2025-04-24 [?] CRAN (R 4.5.0)
 P sessioninfo     1.2.3   2025-02-05 [?] CRAN (R 4.5.0)
 P sf            * 1.0-21  2025-05-15 [?] CRAN (R 4.5.0)
 P shiny           1.10.0  2024-12-14 [?] CRAN (R 4.5.0)
 P stringi         1.8.7   2025-03-27 [?] CRAN (R 4.5.0)
 P stringr       * 1.5.1   2023-11-14 [?] CRAN (R 4.5.0)
 P terra           1.8-54  2025-06-01 [?] CRAN (R 4.5.0)
 P tibble          3.2.1   2023-03-20 [?] CRAN (R 4.5.0)
 P tidyr         * 1.3.1   2024-01-24 [?] CRAN (R 4.5.0)
 P tidyselect      1.2.1   2024-03-11 [?] CRAN (R 4.5.0)
 P timechange      0.3.0   2024-01-18 [?] CRAN (R 4.5.0)
 P tzdb            0.5.0   2025-03-15 [?] CRAN (R 4.5.0)
 P units           0.8-7   2025-03-11 [?] CRAN (R 4.5.0)
 P urlchecker      1.0.1   2021-11-30 [?] CRAN (R 4.5.0)
 P usethis         3.1.0   2024-11-26 [?] CRAN (R 4.5.0)
 P vctrs           0.6.5   2023-12-01 [?] CRAN (R 4.5.0)
 P viridis         0.6.5   2024-01-29 [?] CRAN (R 4.5.0)
 P viridisLite     0.4.2   2023-05-02 [?] CRAN (R 4.5.0)
 P vroom           1.6.5   2023-12-05 [?] CRAN (R 4.5.0)
 P withr           3.0.2   2024-10-28 [?] CRAN (R 4.5.0)
 P xfun            0.52    2025-04-02 [?] CRAN (R 4.5.0)
 P xml2            1.3.8   2025-03-14 [?] CRAN (R 4.5.0)
 P xtable          1.8-4   2019-04-21 [?] CRAN (R 4.5.0)
 P yaml            2.3.10  2024-07-26 [?] CRAN (R 4.5.0)
 P zip             2.3.3   2025-05-13 [?] CRAN (R 4.5.0)

 [1] /home/steffi/Projects/vulture_migration/renv/library/linux-ubuntu-noble/R-4.5/x86_64-pc-linux-gnu
 [2] /home/steffi/.cache/R/renv/sandbox/linux-ubuntu-noble/R-4.5/x86_64-pc-linux-gnu/9a444a72

 * ── Packages attached to the search path.
 P ── Loaded and on-disk path mismatch.

──────────────────────────────────────────────────────────────────────────────
Back to top